Question

NO LINKS!! URGENT HELP PLEASE!! Find the measure of line segment CE part 2​

Answer 1

CE = 20

Explanation:

7x12=6(3x+5)

84= 18x+30

54 = 18x

x=3

CE = 6 + 3(3) +5

CE = 20

Answer 2

`\overline{\sf CE}=20`

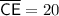
Explanation:

The Intersecting Chords Theorem states that when two chords intersect inside a circle, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.

In the given diagram, chord CE intersects the chord BD at point L.

Therefore, according to the Intersecting Chords Theorem:

`\sf \overline{CL} \cdot \overline{LE} = \overline{BL} \cdot \overline{LD}`

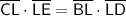
Substitute the values and expression of each segment into the equation:

`6 \cdot (3x+5)=7 \cdot 12`

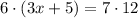
Solve for x:

`18x+30=84`

`18x+30-30=84-30`

`18x=54`

`(18x)/(18)=(54)/(18)`

`x=3`

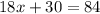
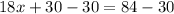
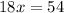
The measure of line segment CE is the sum of line segments CL and LE. Therefore:

`\sf \overline{CE}=\overline{CL}+\overline{LE}`

`\overline{\sf CE}=6+(3x+5)`

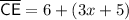
Substitute the found value of x into the equation:

`\overline{\sf CE}=6+(3(3)+5)`

`\overline{\sf CE}=6+(9+5)`

`\overline{\sf CE}=6+14`

`\overline{\sf CE}=20`

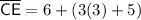
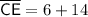
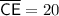
Therefore, the measure of line segment CE is 20 units.