Answer:
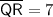
Explanation:
A secant is a straight line that intersects a circle at two points.
A segment is part of a line that connects two points.
The given diagram shows two secant segments US and QS that intersect at exterior point S. Their external parts are TS and RS, respectively.
To find the measure of line segment QR, we first need to find the value of x. To do this, we can use the Intersecting Secants Theorem.
The Intersecting Secants Theorem states that the product of the measures of one secant segment and its external part is equal to the product of the measures of the other secant segment and its external part.
Therefore, according to the Intersecting Secants Theorem:
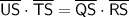
Substitute the value or expression of each segment into the equation and solve for x:
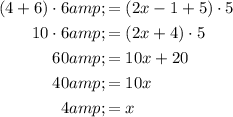
Therefore, the value of x is 4.
To determine the measure of line segment QR, substitute the found value of x into the expression for the line segment:
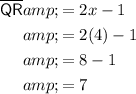
Therefore, the measure of line segment QR is 7 units.