Question

Cos^4(x)Sin^2(x) in terms of cosine

Answer 1

cos⁴(x) - cos⁶(x)

Explanation:

To write the given trigonometric expression in terms of cosine, we'll use trigonometric identities to express sine in terms of cosine. The key identity we'll use is the Pythagorean identity:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Pythagorean Identity:}}\\\\ \sin^2A+\cos^2A=1\\\\ \rightarrow\boxed{\sin^A=1-\cos^2A}\end{array}\right}`

Our given trigonometric expression:

`\cos^4(x)\sin^2(x)`

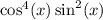
Now, substitute the identity into the expression:

`\cos^4(x)\sin^2(x)\\\\\\\\\Longrightarrow \cos^4(x)(1- \cos^2(x))`

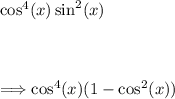
Now, let's simplify this expression by distributing the cos⁴(x):

`\cos^4(x)(1- \cos^2(x))\\\\\\\\\Longrightarrow \boxed{\boxed{\cos^4(x)- \cos^6(x)}}`

Thus, the given trigonometric expression is written in terms of cosine.

`\hrulefill`

Additional Information:

Trigonometric Functions: Trigonometric functions are mathematical functions used in geometry and calculus to relate the angles of a triangle to the lengths of its sides. The primary trigonometric functions are sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot).

Trigonometric Identities: Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables within their domains. They are crucial tools in trigonometry for simplifying expressions and solving equations. In this case, we used the Pythagorean identity to rewrite Sin^2(x) in terms of Cos^2(x).

Pythagorean Identity: One of the fundamental trigonometric identities is the Pythagorean identity, which states that for any angle x in a right triangle:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Pythagorean Identity:}}\\\\ \sin^2A+\cos^2A=1\end{array}\right}`

Simplifying Expressions: When simplifying trigonometric expressions, it's essential to be familiar with basic algebraic techniques such as factoring and expanding. Distributing, as shown in the solution, involves multiplying each term inside parentheses by the term outside.