Question

Solve the inequality
-1/3w>6
-

Answer 1

• 
  `\sf{w < -18}`

In-depth explanation:

Hi! The question is asking us to solve the inequality.

`\sf{-(1)/(3)w > 6}`

Multiply both sides by 3:

`\sf{-1w > 18}`

Reverse the inequality sign:

`\sf{w < -18}`

Therefore, w < -18.

Answer 2

w < -18

Explanation:

To solve the given inequality, you need to find the values of "w" that satisfy the inequality. The goal is to isolate "w" on one side of the inequality symbol.

`\hrulefill`

Given inequality:

`-(1)/(3)w > 6`

Get rid of the fraction by multiplying both sides by -3. When multiplying or dividing an inequality by a negative number, the inequality sign flips.

`-(1)/(3)w > 6\\\\\\\\\Longrightarrow -3\cdot -(1)/(3)w > -3 \cdot 6\\\\\\\\\therefore \boxed{\boxed{w < -18}}`

`\hrulefill`

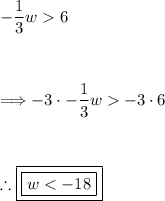
Additional Information:

Inequality: An inequality is a mathematical expression that shows a relationship between two quantities, stating that one is greater than, less than, greater than or equal to, less than or equal to, or not equal to the other.

Isolate: In the context of solving an inequality, "isolating" a variable means to get it on one side of the inequality symbol by performing operations (such as addition, subtraction, multiplication, or division) on both sides of the inequality.

Fraction: A fraction represents a part of a whole and is written in the form of "numerator/denominator." The numerator represents the number of parts being considered, and the denominator represents the total number of equal parts in the whole.

Multiplying or Dividing by a Negative Number: When you multiply or divide an inequality by a negative number, the inequality sign must be flipped. For example, if you have the inequality "x > 3," and you multiply both sides by -1, you get "-x < -3."

Remember, when solving inequalities, it's essential to follow the same rules as solving equations, but keep in mind the rules for handling inequalities when multiplying or dividing by negative numbers. Additionally, if you need to graph the solution on a number line, you would shade the region to the left of -18 since we have 'w < -18'.