Question

How would I solve this word problem?

Answer 1

705 ft

Explanation:

To estimate the height of the building, we can use trigonometry, specifically the tangent function, which relates the angle of elevation to the height and distance.

Let's call the height of the building "h," the initial distance from the students to the building "d," and "x" the distance the students are from the building when the angle is 52°. We are given two angles of elevation, 39° and 52°, and we know that the students moved 320 feet closer to the building for the second measurement.

`\hrulefill`

(1) - Draw a diagram. Refer to the attached image.

(2) - Set up the first equation for triangle ACD:

In the first scenario, when the angle of elevation is 39°, the tangent of the angle can be represented as follows:

`\Longrightarrow \tan(39\°) = (h)/(d)\\\\\\\\\Longrightarrow \tan(39\°) = (h)/(x+320)`

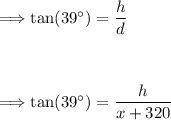
Solving for "h," we have:

`\Longrightarrow \boxed{h = \tan(39\°)(x+320)}`

(3) - Set up the second equation for triangle BCD:

In the second scenario, when the angle of elevation is 52°, the students are 320 feet closer to the building, and are "x" feet away from the base of the building. The tangent of the angle can be represented as follows:

`\Longrightarrow \tan(52\°) = (h)/(x)`

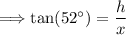
Solving for "h," we have:

`\Longrightarrow \boxed{h = x\tan(52\°)}`

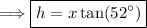
(4) - Solve the equations:

Now, we have two equations with two unknowns (h and d). We can solve these equations simultaneously to find the values of "h" and "x."

We can solve this system of equations by setting the equations equal to each other and solving for the value of "x."

`\Longrightarrow \left\{\begin{array}{ccc}h = \tan(39\°)(x+320)\\\\h = x\tan(52\°)\end{array}\right\\\\\\\\\Longrightarrow \tan(39\°)(x+320) =x\tan(52\°)\\\\\\\\\Longrightarrow x\tan(39\°)+320\tan(39\°) =x\tan(52\°)\\\\\\\\\Longrightarrow 0.809784x+259.131 =1.27994x\\\\\\\\\Longrightarrow 0.470158x = 259.131\\\\\\\\\therefore \boxed{x \approx551 \ ft}`

(5) - Estimate the height of the building:

We found the value of "x" plug this into either of the two equations we derived to find "h," the height of the building.

`\Longrightarrow h=(551)\tan(52 \textdegree)\\\\\\\\\therefore \boxed{\boxed{h \approx 705 \ ft}}`

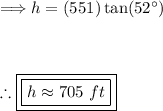
Thus, the height of the building is approximately 705 feet rounded to the nearest foot.

`\hrulefill`

Additional Information:

Angle of Elevation: The angle of elevation is the angle between the horizontal plane (in this case, the street level) and the line of sight from the observer to the top of an object (in this case, the top of the building).

Tangent Function: In trigonometry, the tangent function (tan) is defined as the ratio of the length of the side opposite an angle to the length of the adjacent side. For a right-angled triangle, it can be calculated as follows:

⇒ tan(θ) = opposite side / adjacent side

Right Triangle: A right-angled triangle is a type of triangle that has one angle measuring 90° (a right angle). The side opposite the right angle is called the hypotenuse, and the other two sides are called the legs.

Trigonometric Ratios: In addition to the tangent function, there are two other primary trigonometric ratios: sine (sin) and cosine (cos). In this problem, we are using the tangent function because we have the angle of elevation and the distance from the building (we weren't given the hypotenuse).

⇒ sin(θ) = opposite side / hypotenuse side

⇒ cos(θ) = adjacent side / hypotenuse side

Estimation: The final answer requires rounding the height of the building to the nearest foot, as the initial measurements and calculations may not be precise enough to provide an exact value.