Question

Question 1. Find the number B, such as the average rate of change of f on the interval.

Answer 1

b = 9

Explanation:

To find the number "b" such that the average rate of change of the function
`f(x) = (1)/(x)` on the interval [2, b] is -1/18, we need to calculate the average rate of change and then set it equal to -1/18.

The average rate of change of a function on an interval [a,b] is defined as the change in the function's value divided by the change in the input variable (in this case, x) over the interval. Mathematically, it is given by:

`\rightarrow Avg. = (f(b)-f(a))/(b-a)`

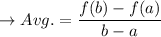
Where:

• f(b) represents the value of the function at x = b

• f(a) represents the value of the function at x = a

`\hrulefill`

In our case,
`f(x) = (1)/(x)`, and the interval is [2, b]. So, a = 2 and b = b.

Now, we need to calculate f(a) and f(b):

For f(a); a = 2:

`\Longrightarrow f(a) = (1)/(a)\\\\\\\Longrightarrow f(2) = \boxed{ (1)/(2)}`

For f(b); a = b:

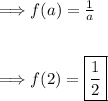
`\Longrightarrow f() = \boxed{(1)/(b)}`

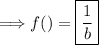
Next, we can plug all this information into the average rate of change formula:

`\Longrightarrow -(1)/(18) = ((1)/(b) -(1)/(2) )/(b-2)`

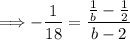
Now, we can solve for "b." To do this, we can first cross-multiply to eliminate the fractions:

`\Longrightarrow b-2 = -18\Big((1)/(b) -(1)/(2)\Big)`

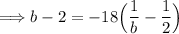
Expand the right side of the equation and simplify:

`\Longrightarrow b-2 = -18 \cdot (1)/(b) -(-18)\cdot(1)/(2)\\\\\\\\\Longrightarrow b-2 = -(18)/(b) +9`

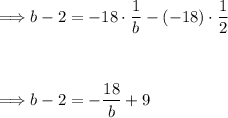
Now, let's get rid of the fractions by multiplying everything by b (the common denominator):

`\Longrightarrow b\Big[b-2 = -(18)/(b) +9\\\\\\\\\Longrightarrow b^2-2b = -18 +9b`

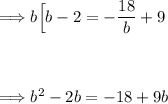
Move all the terms to one side to set the equation to zero:

`\Longrightarrow b^2-2b+18-9b = 0`

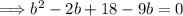
Combine like terms:

`\Longrightarrow b^2-11b+18 = 0`

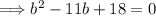
Now we need to solve this quadratic equation for "b." We can either factor or use the quadratic formula. I will factor:

`\Longrightarrow (b-2)(b-9) = 0`

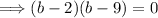
From this, we get two potential solutions: b = 2 or b = 9.

However, we need to check if both of these solutions satisfy the condition for the average rate of change to be -1/18.

For b = 2:

`\Longrightarrow -(1)/(18) = ((1)/(b) -(1)/(2) )/(b-2)\\\\\\\\\Longrightarrow -(1)/(18) = ((1)/(2) -(1)/(2) )/(2-2)\\\\\\\\\Longrightarrow -(1)/(18) \\eq 0`

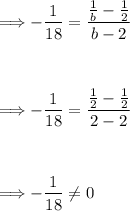
For b = 9:

`\Longrightarrow -(1)/(18) = ((1)/(b) -(1)/(2) )/(b-2)\\\\\\\\\Longrightarrow -(1)/(18) = ((1)/(9) -(1)/(2) )/(9-2)\\\\\\\\\Longrightarrow -(1)/(18) = (-(7)/(18) )/(7)\\\\\\\\\Longrightarrow -(1)/(18) = -(1)/(18)`

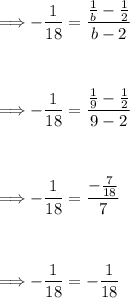
Thus, the correct value for "b" that satisfies the condition is b = 9.

`\hrulefill`

Additional Terminology:

Average Rate of Change: The average rate of change of a function over an interval measures the average rate at which the function's output values (y-values) change concerning the input values (x-values) within that interval. It represents the slope of the secant line between two points on the function's graph corresponding to the interval endpoints.

Interval Notation: In mathematics, interval notation is used to describe a range of values. The interval [2, b] represents all the values of "x" that lie between 2 and "b," including both 2 and "b." The square brackets denote that the endpoints 2 and "b" are included in the interval.

Factoring: A method used to find the roots (solutions) of a quadratic equation by rewriting it as a product of binomials.

Roots/Solutions: The values of the variable that satisfy the equation and make it true.