Question

For each of the following functions, determine whether it is even, odd or neither: (a) x2−2, (b) x3sin2x, (c) cosxsin3x, (d) xex

Answer 1

1. even

2. even

3. odd

4. neither

Explanation:

A function is even if

`f(x) = f( - x)`

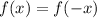
A function is odd if

`f( - x) = - f( x)`

A, A is a quadratic, and all quadratic are even so A is even.

However, let's do the work

`f(x) = {x}^(2) - 2`

`f( - x) = ( - x) {}^(2) - 2 = {x}^(2) - 2`

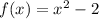
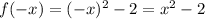
Thus the function is even.

For b,

`f(x) = {x}^(3) \sin(2x)`

Is the function is even?

`f( - x) = ( { - x}^(3) ) \sin( - 2x) = - {x}^(3) * - \sin(2x) = {x}^(3) \sin(2x)`

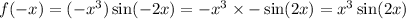
So the function is even.

For c,

`f(x) = \cos(x) \sin(3x)`

Is the function even?

`f( - x) = \cos( - x) \sin( - 3x) = - \cos(x) \sin(3x)`

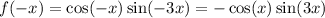
So the function is not even.

`- f(x) = - \cos(x) \sin(3x)`

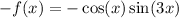
Notice that -f(x) and f(-x) are equal, thus the function is odd.

d.

`f(x) = x {e}^(x)`

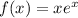
Is the function even?

`f( - x) = - xe {}^( - x)`

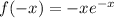
Is the function odd?

`- f(x) = - xe {}^(x)`

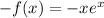
So the function is neither even or odd.