Question

Help me please..
x+4 1
6x =. X

Answer 1

Hello!

Answer:

`\Large \boxed{\sf x = 2}`

Explanation:

We want to solve this equation:

`\sf (x+4)/(6x) = (1)/(x)`

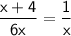
Let's isolate x.

◼ Multiply both sides by x:

`\sf (x+4)/(6x) * x= (1)/(x) * x`

◼ Simplify both sides:

`\sf (x(x+4))/(6x) = 1`

◼ Simplify the left side:

`\sf (x^2+4x)/(6x) = 1`

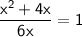
◼ Multiply both sides by 6x:

`\sf (x^2+4x)/(6x) * 6x = 1 * 6x`

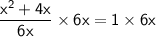
◼ Simplify both sides:

`\sf x^2+4x =6x`

◼ Subtract 6x from both sides:

`\sf x^2+4x-6x =6x-6x`

◼ Simplify both sides:

`\sf x^2 -2x=0`

It's a quadratic equation because the equation is in the form ax² + bx + c = 0.

The value of x in a quadratic formula is equal to:

`\sf x = (-b \pm √(b^2 -4ac) )/(2a)`

In our equation:

`\sf a =1\\b =-2\\c =0`

Let's solve this quadratic equation:

`\sf x = (-(-2) \pm √((-2)^2 -4 * 1 * 0) )/(2 * 1)`

◼ Simplify the right side:

`\sf x = (2 \pm2 )/(2)`

◼ Find the solutions:

`\sf x = (2+2 )/(2) = (4)/(2) = 2 \\\\\\\sf x = (2 -2 )/(2) = (0)/(2) = 0`

We can't divide by 0 if we replace x by 0 in our equation.

So, the solution of our equation is 2.