Answer:
Approximately
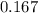 (assuming the ice is level and that
(assuming the ice is level and that
 .)
.)
Step-by-step explanation:
The coefficient of kinetic friction is equal to the ratio between the magnitude of kinetic friction and normal force. To find the coefficient of kinetic friction in this question, it will be necessary to find both the kinetic friction and the normal force.
Under the assumptions, the normal force between the ice and the hockey puck would be equal to the weight of the puck. The weight of this puck can be expressed in terms of the mass of the puck and the gravitational field strength
 .
.
Since all other forces on the hockey puck would be balanced, the net force on the puck would be equal to kinetic friction. The net force on the puck can be found by multiplying the mass of the puck by acceleration, where the acceleration can be found from velocity and displacement using SUVAT equations.
Divide the magnitude of kinetic friction by the magnitude of normal force to find the coefficient of kinetic friction.
Let
 denote the mass of this puck. The weight of this puck would be
denote the mass of this puck. The weight of this puck would be
 . Assuming that the ice surface is level, the magnitude of the normal force on this puck would be equal to that of the weight of the puck:
. Assuming that the ice surface is level, the magnitude of the normal force on this puck would be equal to that of the weight of the puck:
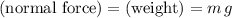 .
.
It is given that the puck has slowed down from an initial velocity of
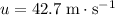 to a velocity of
to a velocity of
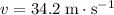 . The change in position is
. The change in position is
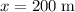 . The acceleration
. The acceleration
 of this puck can be found using the SUVAT equation
of this puck can be found using the SUVAT equation
 :
:
 .
.
Multiply the acceleration of the puck by its mass to find the net force on the puck:
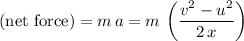 .
.
Assuming that the surface is level, kinetic friction would be the only unbalanced force on this puck. Hence, the net force on the puck would be equal to the kinetic friction on the puck:
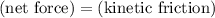 .
.
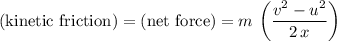 .
.
To find the coefficient of kinetic friction
 , divide the magnitude of kinetic friction by the magnitude of the normal force:
, divide the magnitude of kinetic friction by the magnitude of the normal force:
 .
.
In other words, the coefficient of kinetic friction between the two surfaces would be approximately
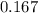 .
.