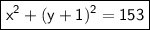Question

Write the equation of a circle with its diameter whose endpoints are (-3, 11) and (3, -13).

Answer 1

`\sf \textsf{ Equation of Circle is:}\boxed{\sf x^2 + (y +1 )^2 = 153}`

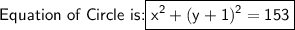
Explanation:

Given:

Endpoints are (x1,y1)=(-3, 11) and (x2,y2)=(3, -13).

First we need to find center,

As the midpoint of the diameter is the center of the circle.

We can find the midpoint using the midpoint formula:

`\boxed{\textsf{ midpoint or center (h,k)}\sf = ((x_1 + x_2))/(2), ((y_1 + y_2))/(2)}`

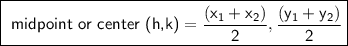
In this case, the midpoint is:

`\textsf{ midpoint or center (h,k)}\sf = ((-3+ 3))/(2), ((11+ (-13)))/(2)=(0,-1)`

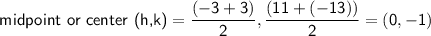
Now, Let's find the radius,

The radius of the circle is the distance from the center of the circle to one of the endpoints of the diameter.

We can find the radius using the distance formula:

`\textsf{distance } \sf = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2`

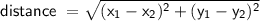
In this case, the radius is:

`\sf radius(r) = √((3 - 0)^2 + (13 -1)^2) )= √(9+144) = √(153)`

Substitute the information into the circle formula:

The circle formula is:

`\boxed{\sf (x - h)^2 + (y - k)^2 = r^2}`

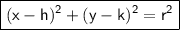
where:

• h and k is the x-coordinate and y coordinate of the center of the circle respectively
• r is the radius of the circle

In this case, we have:

`\sf (h,k) =(0,-1)`

`\sf r = √(153)`

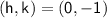
Substituting these values into the circle formula, we get the equation:

`\tt (x - 0)^2 + (y - (-1))^2 = (√(153))^2`

`\sf x^2 + (y +1 )^2 = 153`

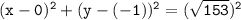
Therefore,

The equation of the circle with its diameter whose endpoints are (-3, 11) and (3, -13) is:

`\boxed{\sf x^2 + (y +1 )^2 = 153}`