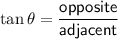Question

100 POINTS!!!! JUST LOOK

please give simple step by step reasons for each answer or just as many as you can pls. anything is helpful.

Answer 1

`\textsf{1)}\quad \sf \overline{PR}=\overline{QS}=20`

`\textsf{2)} \quad \sf Area\;\triangle PQR = 50√(3) \approx 86.6 \;square \;units`

`\textsf{3)} \quad \sf Area\; \boxed{\phantom{w}}\; PQRS = 100√(3) \approx 173.2 \;square \;units`

`\textsf{4A)} \quad \sin (\sf PRS)=\sf (10)/(20)=(1)/(2)`

`\textsf{4B)} \quad \cos(\sf PRQ)=\sf (10)/(20)=(1)/(2)`

`\textsf{4C)} \quad \tan(\sf PQS)=\sf (10)/(10√(3))=(√(3))/(3)`

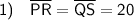
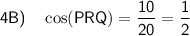
Explanation:

Problem #1

The given figure PQRS is a rectangle.

As the diagonals of a rectangle are congruent and bisect each other (divide into two equal parts), TR = PT and PR = QS.

Given that PT = 10, we can say that:

`\sf \overline{TR}=\overline{PT}=10`

As PR = PT + TR:

`\sf \overline{PR}=\overline{PT}+\overline{TR}=10+10=20`

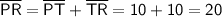
Finally, as PR = QS:

`\sf \overline{QS}=\overline{PR}=20`

Therefore,
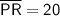`\sf \overline{PR} = 20` and
`\sf \overline{QS} = 20`.

`\hrulefill`

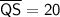Problem #2

As PQRS is a rectangle, all interior angles are right angles. Therefore:

`\sf m\angle PQR = m\angle QRS = m\angle RSP = m\angle SPQ = 90^(\circ)`

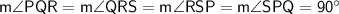
As angle SPR is 60°, then m∠QPR = 30°.

This means that the third angle in triangle PQR, angle QRP, is 60°.

Therefore, triangle PQR is a 30-60-90 right triangle with hypotenuse PR.

In a 30-60-90 triangle, the shortest leg is half the measure of the hypotenuse, and the longer leg is √3 times the measure of the shortest leg. As QR is the shortest leg (since it is opposite the 30° angle), and PQ is the longest leg (since it is opposite the 60° angle), then:

`\sf \overline{QR}=(20)/(2)=10`

`\sf \overline{PQ}=10√(3)`

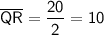
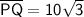
The area of a right triangle is the half the product of its legs. Therefore:

`\begin{aligned}\sf Area\;of \;\triangle PQR&= \sf (1)/(2) \overline{QR}\cdot \overline{PQ}\\\\&=\sf (1)/(2) 10 \cdot 10√(3)\\\\&=\sf 5 \cdot 10√(3)\\\\&=\sf 50√(3)\\\\&\approx \sf 86.602540...\\\\&\approx \sf 86.6\; square\;units\;(nearest\;tenth)\end{aligned}`

Therefore, the area of triangle PQR is exactly 50√3 square units, or approximately 86.6 square units (rounded to the nearest tenth).

`\hrulefill`

Problem #3

The area of a rectangle is the product of its width and length.

The width of rectangle PQRS is QR, and its length is PQ.

As we have already determined the measures of QR and PQ in the previous step, then:

`\begin{aligned}\sf Area\;of\;rectangle\;PQRS&=\sf \overline{QR} \cdot \overline{PQ}\\&=\sf 10 \cdot 10√(3)\\&=\sf 100√(3)\\&\approx \sf 173.20508...\\&\approx \sf 173.2\; square\;units\;(nearest\;tenth)\end{aligned}`

Therefore, the area of rectangle PQRS is exactly 100√3 square units, or approximately 173.2 square units (rounded to the nearest tenth).

`\hrulefill`

Problem #4A

The sine ratio is the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse.

The side opposite ∠PRS is PS, which is equal in length to side QR. Therefore, PS = 10.

The hypotenuse of ΔPRS is PR = 20.

Substitute these values into the sine ratio:

`\sin \theta=\sf (opposite)/(hypotenuse)`

`\sin (\sf PRS)=\sf (PS)/(PR)`

`\sin (\sf PRS)=\sf (10)/(20)=(1)/(2)`

`\hrulefill`

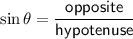
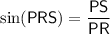
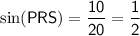
Problem #4B

The cosine ratio is the ratio of the length of the side adjacent an angle in a right triangle to the length of the hypotenuse.

The side adjacent ∠PRQ is QR = 10.

The hypotenuse of ΔPRQ is PR = 20.

Substitute these values into the cosine ratio:

`\cos \theta=\sf (adjacent)/(hypotenuse)`

`\cos(\sf PRQ)=\sf (QR)/(PR)`

`\cos(\sf PRQ)=\sf (10)/(20)=(1)/(2)`

`\hrulefill`

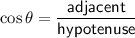
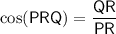
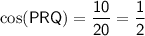
Problem #4C

The tangent ratio is the ratio of the length of the side opposite an angle in a right triangle to the length of the side adjacent to that angle.

The side opposite ∠PQS is PS, which is equal in length to side QR. Therefore, PS = 10.

The side adjacent ∠PQS is PQ, which is 10√3 in length. Therefore, PQ = 10√3.

Substitute these values into the tangent ratio:

`\tan\theta=\sf (opposite)/(adjacent)`

`\tan(\sf PQS)=\sf (PS)/(PQ)`

`\tan(\sf PQS)=\sf (10)/(10√(3))=(1)/(√(3))=(1 \cdot √(3))/(√(3) \cdot √(3))=(√(3))/(3)`