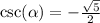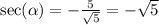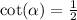1 Answer

Lahar Shah · Answer 1 · 2024-07-26T02:13:10+0000

Explanation:

The trigonometric ratios for a point that lies on the terminal arm are

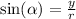
$\sin( \alpha ) = (y)/(r)$

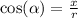
$\cos( \alpha ) = (x)/(r)$

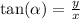
$\tan( \alpha ) = (y)/(x)$

Where r is defined as

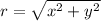
$r = \sqrt{ {x}^(2) + {y}^(2) }$

This means that r must be nonnegative

So for the point (-3,-6), the one that must be positive is tan and the ones that are negative are sin and cos.

b.

The reciprocal identities follow as

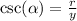
$\csc( \alpha ) = (r)/(y)$

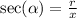
$\sec( \alpha ) = (r)/(x)$

$\cot( \alpha ) = (x)/(y)$

So the reciprocal will be the same as well.

So the one that will be positive are cotangent and the ones that are negative are sec and csc.

c. Using the primary trig ratio, we know that

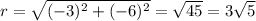
$r = \sqrt{( - 3 ){}^(2) + ( - 6) {}^(2) } = √(45) = 3 √(5)$

So the trigonometric primary ratios are

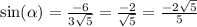
$\sin( \alpha ) = ( - 6)/(3 √(5) ) = ( - 2)/( √(5) ) = ( - 2 √(5) )/(5)$

$\cos( \alpha ) = - (3)/(3 √(5) ) = - ( √(5) )/(5)$

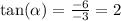
$\tan( \alpha ) = ( - 6)/( - 3) = 2$

For the reciprocal ratios,

$\csc( \alpha ) = - ( √(5) )/(2)$

$\sec( \alpha ) = - (5)/( √(5) ) = - {√(5) }{}$

$\cot( \alpha ) = (1)/(2)$

Please log in or register to add a comment.