Question

I am so confused, please help! :)

Answer 1

X = 8 , Z= 1 , Y = 6

Explanation:

given that,

(32a^2 + 24b^2)/4ab = Xa/b + Yb/Za

(32a^2 + 24b^2)/4ab = 32a^2/4ab + 24b^2/4ab

32a^2/4ab = 8a/b

24b^2/4ab = 6b/a

now,

8a/b = Xa/b

so X = 8

6b/a = Yb/Za

so Y = 6 and Z =1

Answer 2

`X = \boxed{8}`

`Y = \boxed{6}`

`Z = \boxed{1}`

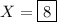
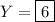
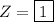
Explanation:

Given equation:

`(32a^2+24b^2)/(4ab)=(Xa)/(b)+(Yb)/(Za)`

To find the values of X, Y and Z, add the fractions on the right side of the equation, then equate the numerators and denominators.

Add the fractions on the right side of the equation using the fraction rule:

`\boxed{(p)/(q)+(s)/(t)=(pt+qs)/(qt)}`

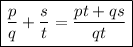
Therefore:

`(32a^2+24b^2)/(4ab)=(Xa\cdot Za+b\cdot Yb)/(b\cdot Za)`

`(32a^2+24b^2)/(4ab)=(XZa^2+Yb^2)/(Zab)`

As the coefficients of the terms on the left side of the equation are all multiples of 4, we can reduce the fraction on the left side to its simplest form by dividing each term by 4 to give:

`(8a^2+6b^2)/(ab)=(XZa^2+Yb^2)/(Zab)`

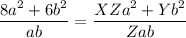
Now, equate the denominators and solve for Z:

`\begin{aligned}ab&=Zab\\1&=Z\\ Z&=1\end{aligned}`

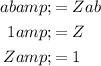
Equate the numerators and substitute the found value of Z:

`8a^2+6b^2=XZa^2+Yb^2`

`8a^2+6b^2=Xa^2+Yb^2`

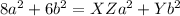
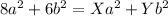
Solve for X by equating the a² terms :

`\begin{aligned}8a^2&=Xa^2\\8&=X\\X&=8\end{aligned}`

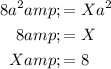
Solve for Y by equating the b² terms :

`\begin{aligned}6b^2&=Yb^2\\6&=Y\\Y&=6\end{aligned}`

Therefore, the values of the capitalised pronumerals are:

• X = 8
• Y = 6
• Z = 1