Question

What is the cube root of 6^27?

Answer 1

`b^(9)`

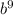
Explanation:

The cube root of b^27 can be found by using the property of exponents that says (a^n)^m = a^(n×m), which means that we can rewrite b^27 as (b^3)^9.

Therefore, the cube root of b^27 is:

∛(b^27) = ∛((b^3)^9)

Using the property of cube roots that says ∛(a^3) = a, we can simplify this expression as:

∛((b^3)^9) = b^(3×9) = b^27

Therefore, the cube root of b^27 is simply b^9.