Answer: y =
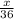 , y = -
, y = -
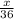
Explanation:
Every hyperbola has two asymptotes. We can use the formula to solve for these asymptotes. We are given the equation 1296y² - x² = 81.
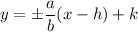
We will substitute our values into the formula. (h, k), the center of the hyperbola, is at (0, 0) here.
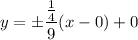
Now, we can simplify by multiplying, distributing, subtracting, adding, etc.
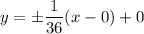
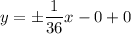
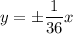
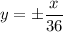
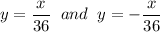
I have attached a graph of this below. The hyperbola is graphed in blue with the asymptotes graphed in red.