Question

Simplify the expression \frac{\tan x + \cot x}{\cot x}

Answer 1

2

Explanation:

Given the trigonometric expression:

`(\tan(x) + \cot(x))/(\cot(x))`

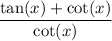
We can first expand by splitting it into two fractions:

`(\tan(x))/(\cot(x)) + (\cot(x))/(\cot(x))`

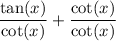
The second term is equal to 1:
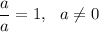`(a)/(a) = 1, \ \ a \\e 0`; hence:

`(\tan(x))/(\cot(x)) + 1`

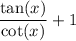
Next, we can rewrite the trigonometric ratios in the first term as their definitions:
`\tan(x) = (\sin(x))/(\cos(x))`,
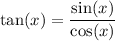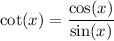`\cot(x) = (\cos(x))/(\sin(x))`; hence:

`(\ \, (\sin(x))/(\cos(x))\ \,)/((\cos(x))/(\sin(x))) + 1`

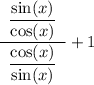
And this division of fractions can be represented as the multiplication by the reciprocal of the divisor:

`(\sin(x))/(\cos(x))\cdot (\cos(x))/(\sin(x)) + 1`

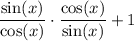
We can see that both sin(x) and cos(x) cancel in the numerator and denominator, leaving the value of the first term as 1:

`1+1`

So, the simplified form of the trigonometric expression:

`(\tan(x) + \cot(x))/(\cot(x))`

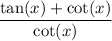
is 2.