Question

Line 1: 4y= 3x+7 Line 2: 8x+6y=8 3 Line 3: y=-x-6 4 1 For each pair of lines, determine whether they are parallel, perpendicu Line 1 and Line 2: O Parallel O Perpendicular O Neither Line 1 and Line 3: O Parallel O Perpendicular O Neither Line ​

Answer 1

Line 1 and Line 2: Perpendicular

Line 1 and Line 3: Parallel

Line 2 and Line 3: Perpendicular

Explanation:

Consider two lines
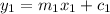`y_1 = m_1x_1+c_1` and
`y_2 = m_2x_2+c_2`

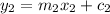
If m₁ = m₂ then these lines are parallel

If
`m_1 = -(1)/(m_2)` then the lines are perpendicular

We can rewrite the given lines in the form of : y = mx + c as follows

Line 1:

`4y=3x+7\\\\\Rightarrow y = (3)/(4)x+(7)/(4)`

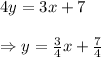
Line 2:

`8x+6y=8\\\\\Rightarrow 6y = -8x+8\\\\\Rightarrow y = -(8)/(6)x+(8)/(6)\\\\\Rightarrow y = -(4)/(3)x+(4)/(3)`

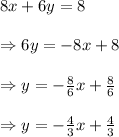
Line 3:

`y = (3)/(4)-6`

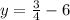
Comparing Line 1 and Line 2:

`\text{Line 1:}y = (3)/(4)x+(7)/(4)\\\\\text{Line 2:}y = -(4)/(3)x+(4)/(3)\\\\m_1 = (3)/(4)\\\\m_2 = -(4)/(3)\\\\m_1 = -(1)/(m_2)`

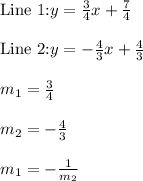
∴ Line 1 and Line 2: Perpendicular

Comparing Line 1 and Line 3:

`\text{Line 1:}y = (3)/(4)x+(7)/(4)\\\\\text{Line 3:}y = (3)/(4)x-6\\\\m_1 = (3)/(4)\\\\m_2 = (3)/(4)\\\\m_1 = m_2`

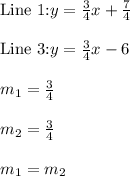
∴ Line 1 and Line 3: Parallel

Comparing Line 2 and Line 3:

`\text{Line 2:}y = -(4)/(3)x+(4)/(3)\\\\\text{Line 3:}y = (3)/(4)x-6\\\\m_1 = -(4)/(3)\\\\m_2 = (3)/(4)\\\\m_1 = -(1)/(m_2)`

∴ Line 2 and Line 3: Perpendicular