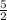Question

If $a + b = 1 and a^2 + b^2 = 2, what is the value of a^3 + b^3? Express your answer as a common fraction.

Answer 1

a³ + b³ =
`(5)/(2)`

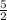
Explanation:

a³ + b³ ← is a sum of cubes and factors in general as

(a + b)(a² - ab + b²)

given

a + b = 1 ← square both sides

(a + b)² = 1² ← expand left side using FOIL

a² + 2ab + b² = 1 ← substitute a² + b² = 2

2ab + 2 = 1 ( subtract 2 from both sides )

2ab = - 1 ( divide both sides by 2 )

ab = -
`(1)/(2)`

substituting into the factored form of a³ + b³

(a + b)(a² - ab + b²)

= 1 (2 - ab)

= 1(2 - (-
`(1)/(2)`) )

= 1(2 +
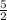
`(1)/(2)` )

= 1 × 2
`(1)/(2)`

= 1 ×
`(5)/(2)`

=
`(5)/(2)`