Question

Solve this..refer to the attachment ​

Answer 1

• X = - 2

Explanation:

`\large{ \longrightarrow \sf{\: ( (5)/(3) ) {}^( - 5) * ( (5)/(3) ) {}^( - 11) = ( (5)/(3) ) {}^(8x) }}`

`\:`

`\large{ \implies \: \sf{ ( (5)/(3) ) {}^( - 5 - 11) = ( (5)/(3) ) {}^(8x) }}`

`\:`

`\large \implies \: \sf{( (5)/(3) ) {}^( - 16) = ( (5)/(3) ) {}^(8x) }`

`\:`

`\large{\implies \: \sf{8x = - 16}}`

`\:`

`\large \implies \: \sf{ x = - (16)/(8) }`

`\:`

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \implies \: \boxed{ \bf{ \pink{x } \blue{= } \purple{ - }\green{2}}}`

Answer 2

Value of x is -2.

Explanation:

Note:

Product of Powers Property: When you have the same base raised to different exponents and they are multiplied together, you can add the exponents.

In mathematical notation, it can be expressed as:

`\sf a^m * a^n = a^(m + n)`

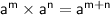
For the Question:

Given expression:

`\sf \left((5)/(3)\right)^(-5) * \left((5)/(3)\right)^(-11) = \left((5)/(3)\right)^(8x)`

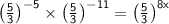
To simplify the left side of the equation, we'll use the rule that states when you multiply two numbers with the same base
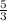`(5)/(3)`, you add their exponents:

`\sf \left((5)/(3)\right)^(-5) * \left((5)/(3)\right)^(-11) = \left((5)/(3)\right)^(-5 + (-11)) = \left((5)/(3)\right)^(-16)`

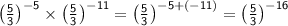
Now, the equation becomes:

`\sf \left((5)/(3)\right)^(-16) = \left((5)/(3)\right)^(8x)`

Now, to solve for x, we can equate the exponents:

`\sf -16 = 8x`

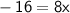
dividing both sides by 8:

`\sf x = (-16)/(8)`

`\sf x = -2`

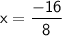
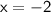
Therefore, Value of x is -2.