Question

What is the maximum distance we can shoot a dart, provided our toy dart gun gives a maximum initial velocity of 7.33 m/s ? More information needed.

5.48 m
3.67 m
10.96 m
​

Answer 1

Approximately
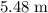`5.48\; {\rm m}` if the dart is launched at an angle of
`45^(\circ)` above the horizon, assuming that air resistance is negligible,
`g = 9.81\; {\rm m\cdot s^(-2)}`, and that the ground is level.

Step-by-step explanation:

The dart in this question is in a projectile motion. To find the maximum range of the dart in under the assumptions, start by finding an expression for range in terms of the angle at which the dart was launched.

To find the expression for the range of the dart, start by decomposing initial velocity into horizontal and vertical components. Make use of the fact that the vertical acceleration of the dart is constant to find the duration of the motion. Since horizontal velocity of the dart is constant, multiplying the duration of the motion by the horizontal velocity of the dart would give the horizontal distance travelled.

Analyze the expression for the range of the dart to find the maximum possible value under these assumptions.

Assume that the dart is to be launched at an angle of
`\theta` above the horizon, where
`0 < \theta \le 90^(\circ)`. Let
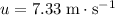`u = 7.33\; {\rm m\cdot s^(-1)}` denote the initial velocity of the dart. Decompose initial velocity into vertical and horizontal components:

• Initial horizontal velocity:
  `u_(x) = u\, \cos(\theta)`.
• Initial vertical velocity:
  `u_(y) = u\, \sin(\theta)`.

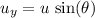Assume that air resistance on the dart is negligible. The horizontal velocity of the dart would stay unchanged during the entire flight. The vertical acceleration of the dart would be constantly
`a_(y) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}`.

During the flight, the vertical velocity of the dart would change from the initial value of
`u_(y)` to
`v_(y) = (-u_(y))` right before landing. In other words, the velocity change in the vertical component would be:

`\begin{aligned}\Delta v_(y) &= v_(y) - u_(y) \\ &= (-u_(y)) - u_(y) \\ &= (-2\, u_(y)) \end{aligned}`.

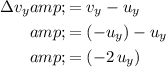Divide the change in the vertical velocity
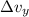`\Delta v_(y)` by the vertical acceleration.
`a_(y)` to find the duration
`t` of the flight:

`\begin{aligned}t &= (\Delta v_(y))/(a_(y)) \\ &= ((-2\, u_(y)))/((-g)) \\ &= (2\, u_(y))/(g) \\ &= (2\, u\, \sin(\theta))/(g)\end{aligned}`.

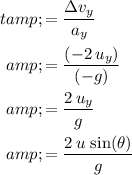Assume that air resistance on the dart is negligible and that the ground is level. The horizontal velocity
`u_(x) = u\, \cos(\theta)` of the dart would be constant. Hence, to find the range
`s` of the dart (horizontal distance travelled,) multiply the duration of the flight
`t` by this horizontal velocity:

`\begin{aligned} s &= u_(x)\, t \\ &= u\, \cos(\theta)\, \left((2\, u\, \sin(\theta))/(g)\right) \\ &= (u^(2)\, (2\, \cos(\theta)\, \sin(\theta)))/(g)\end{aligned}`.

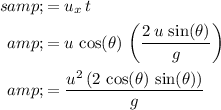Make use of the double angle identity for sine
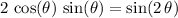`2\, \cos(\theta)\, \sin(\theta) = \sin(2\, \theta)` to simplify the expression for
`s`:

`\begin{aligned} s &= (u^(2)\, (2\, \cos(\theta)\, \sin(\theta)))/(g) \\ &= (u^(2)\, \sin(2\, \theta))/(g)\end{aligned}`.
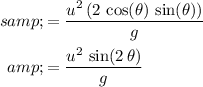Over the range of
`0 < \theta \le 90^(\circ)`, the value of
`2\, \theta` would be in the range
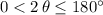`0 < 2\, \theta \le 180^(\circ)`. In that range, the
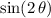`\sin(2\, \theta)` would achieve the maximum value of
`1` when
`2\, \theta = 90^(\circ)`, which requires
`\theta = 45^(\circ)`.

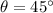In other words, given that
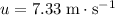`u = 7.33\; {\rm m\cdot s^(-1)}` and
`g = 9.81\; {\rm m\cdot s^(-2)}`, the maximum value for the range under the assumptions would be:

`\begin{aligned} s &=(u^(2))/(g)\\ &= \frac{(7.33\; {\rm m\cdot s^(-1)})^(2)}{(9.81\; {\rm m\cdot s^(-2)})} \\ &\approx 5.48\; {\rm m}\end{aligned}`.

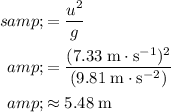This maximum value would be achieved when the projectile is launched at an angle of
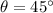`\theta = 45^(\circ)` above the horizon.