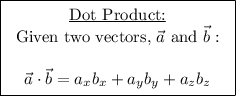Question

Can someone please help me out?
40POINTS 2 QUESTIONS ONLY!

Answer 1

Q1: θ ≈ 25°

Q2: First option, parallel; type "PARALLEL"

Explanation:

To find the cosine of the angle between two planes, we can use the following formula:

`\rightarrow \theta = \cos^(-1)\Big((a_xb_x+a_yb_y+z_xz_y)/(\big|\big|\vec a \big|\big|\big|\big|\vec b \big|\big|)\Big); \ 0\textdegree \leq \theta \leq 180 \textdegree`

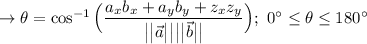
Where vectors a and b are the vectors normal to the given planes.

`\hrulefill`

Q1: Find the cosine of the angle between the planes x + y + z = 0 and x + 3y + 4z = 3.

Step 1: Find the normal vectors of the planes:

For the given plane, x + y + z = 0:

The coefficients of x, y, and z represent the normal vector, so the normal vector is <1, 1, 1>.

For the plane x + 3y + 4z = 3:

The coefficients of x, y, and z represent the normal vector, so the normal vector is <1, 3, 4>.

Step 2: Calculate the dot product of the normal vectors:

⇒ Dot product = (1 · 1) + (1 · 3) + (1 · 4) = 1 + 3 + 4 = 8

Step 3: Calculate the magnitudes of the normal vectors:

⇒ Magnitude of the normal vector of the first plane = √((1)² + (1)² + (1)²) = √3.

⇒ Magnitude of the normal vector of the second plane = √((1)² + (3)² + (4)²) = √26.

Step 4: Find the cosine of the angle between the planes:

`\Longrightarrow \theta = \cos^(-1)\Big((8)/(√(3) \cdot√(26) ) \Big)\\\\\\\\\Longrightarrow \theta = \cos^(-1)\Big((8)/(√(78) ) \Big)\\\\\\\\\therefore \boxed{\theta \approx 25 \textdegree}`
`\hrulefill`

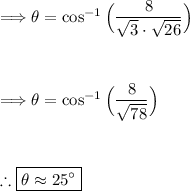
Q2: Determine whether the planes 15x - 6y + 12z = 2 and 4y = 10x + 8z are parallel, perpendicular, or neither.

Step 1: Write both planes in the form Ax + By + Cz = D:

The plane, 15x - 6y + 12z = 2, is already written in this form.

The plane, 4y = 10x + 8z, is rewritten as 10x - 4y + 8z = 0.

Step 2: Find the normal vectors of the planes:

For the plane 15x - 6y + 12z = 2:

The coefficients of x, y, and z represent the normal vector, so the normal vector is <15, -6, 12>.

For the plane 10x - 4y + 8z = 0:

The coefficients of x, y, and z represent the normal vector, so the normal vector is <10, -4, 8>.

Step 3: Check if the normal vectors are parallel or perpendicular:

• Two vectors are parallel if their cross product is the zero vector.

• Two vectors are perpendicular if their dot product is zero.

Taking the cross product:

`\Longrightarrow \left|\begin{array}{ccc}\hat i & \hat j & \hat k\\15& -6&12\\10&-4&8\end{array}\right| = \left|\begin{array}{cc}-6&12\\-4&8\end{array}\right| \hat i \ - \left|\begin{array}{cc}15&12\\10&8\end{array}\right| \hat j \ + \left|\begin{array}{cc}15&-6\\10&-4\end{array}\right| \hat k\\\\\\\\\Longrightarrow [(-6)(8)-(12)(-4)] \hat i - [(15)(8)-(12)(10)] \hat j + [(15)(-4)-(-6)(10)] \hat k`

`\Longrightarrow [-48+48] \hat i - [120-120] \hat j + [-60+60] \hat k\\\\\\\\\Longrightarrow0 \hat i - 0\hat j + 0\hat k \therefore \text{parallel}`

Thus, these planes are parallel. The second box wants you to input PARALLEL.

`\hrulefill`

Additional information:

Normal Vector: The normal vector of a plane is a vector that is perpendicular to the plane. For a plane in the form Ax + By + Cz = D, the normal vector is <A, B, C>.

Cross Product: The cross product of two vectors in three-dimensional space results in a vector that is perpendicular to both of the original vectors. If the cross product of two vectors is the zero vector, it means the vectors are parallel.

Dot Product: The dot product of two vectors is a scalar value that represents the cosine of the angle between the vectors when they are normalized (divided by their magnitudes). If the dot product is zero, the vectors are perpendicular.

`\boxed{\left\begin{array}{ccc}\text{\underline{Dot Product:}}\\\text{Given two vectors,} \ \vec a \ \text{and} \ \vec b:\\\\ \vec a \cdot\vec b = a_xb_x+a_yb_y+a_zb_z \end{array}\right }`