Question

Please help me with this question, thanks.​

Answer 1

Benny has 50 marbles

Explanation:

Let Benny's marbles be x

∴ Ahmad's marbles = x - 35

`(1)/(5) x = (2)/(3)(x - 35)`

∴
`(x)/(5) = (2x - 70)/(3)`

∴3x = 5(2x - 70)

∴3x = 10x - 350

∴350 = 10x - 3x

∴7x = 350

∴ x = 50

∴ Benny has 50 marbles

Answer 2

Hello!

Answer:

`\Large \boxed{\sf 50}`

Explanation:

Let x be the number of Ahmad's marbles. So:

Ahmad =
`\sf x`

Benny =
`\sf x + 35`

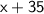
We also know:

`\sf (1)/(5) ~of~ Benny's~ marbles = (2)/(3) ~of ~Amhad's ~marbles`

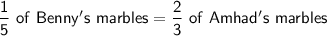
Replace Benny's marbles and Ahmad's marbles by
`\sf x` and
`\sf x + 35`.

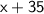Therefore, we have this equation:

`\sf (1)/(5) ~of~ x+35 = (2)/(3) ~of ~x`

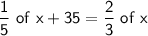
We have just to solve this equation to find the number of Ahmad's marbles for then to find the number of Benny's marbles.

◼ Simplify both sides:

`\sf (x+35)/(5) = (2x)/(3)`

◼ Multiply both sides by 3:

`\sf (x+35)/(5) * 3 = (2x)/(3) * 3`

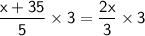
◼ Simplify both sides:

`\sf (3(x+35))/(5) = 2x`

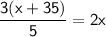
◼ Simplify the fraction:

`\sf (3x+105)/(5) = 2x`

◼ Multiply both sides by 5:

`\sf (3x+105)/(5) * 5 = 2x * 5`

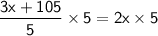
◼ Simplify both sides:

`\sf 3x+105= 10x`

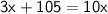
◼ Subtract 3x from both sides:

`\sf 3x+105-3x= 10x -3x`

◼ Simplify both sides:

`\sf 105 = 7x`

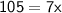
◼ Divide both sides by 7:

`\sf (105)/(7) = (7x)/(7)`

◼ Simplify both sides:

`\sf x = 15`

So the number of Ahmad's marbles is 15.

To find the number of Benny's marbles, we know:

Benny =
`\sf x + 35`

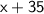
So we have just to replace x by 15:

Benny =
`\sf 15 + 35 = 50`

So the number of Benny's marbles is 50.

Check:

`\sf (1)/(5) ~of~50 = (1 * 50 )/(5) = (50)/(5) = 10`

`\sf (2)/(3) ~of ~15= (2 * 15 )/(3) = (30)/(3) = 10`

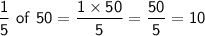
So the equation
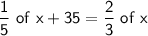`\sf (1)/(5) ~of~ x+35 = (2)/(3) ~of ~x` is verified if x = 15.