Question

A car's bumper is designed to withstand a 5.76 km/h (1.6-m/s) collision with an immovable object without damage to the body of the car. The bumper cushions the shock by absorbing the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.195 m while bringing a 890 kg car to rest from an initial speed of 1.6 m/s.

Answer 1

7319.59 N

Step-by-step explanation:

To calculate the magnitude of the average force on the bumper, we can use the work-energy principle. The work done on the car is equal to the change in its kinetic energy, which is converted into the work done in collapsing the bumper.

The work done by the force on the bumper can be calculated as:

`\text{Work} = \text{Force} * \text{Distance}`

The work done on the car can be calculated using the kinetic energy formula:

`\text{Kinetic Energy} = (1)/(2) * \text{mass} * \text{velocity}^2`

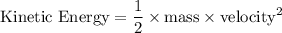
Given:

- Initial velocity of the car (
`v_{\text{initial}}`) = 1.6 m/s

- Final velocity of the car (
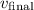`v_{\text{final}}` ) = 0 m/s (car comes to rest)

- Distance the bumper collapses (
`d`) = 0.195 m

- Mass of the car (
`m`) = 890 kg

Step 1: Calculate the change in kinetic energy:

`\Delta \text{KE} = \text{KE}_{\text{final}} - \text{KE}_{\text{initial}}`

`\Delta \text{KE} = 0 - (1)/(2) * m * v_{\text{initial}}^2`

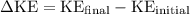
Step 2: Calculate the work done on the car (which is equal to the work done in collapsing the bumper):

`\text{Work} = \Delta \text{KE}`

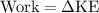
Step 3: Calculate the magnitude of the average force on the bumper:

`\text{Force} = \frac{\text{Work}}{d}`

Now, let's calculate it step by step:

Step 1:

`\Delta \text{KE} = 0 - (1)/(2) * 890 * (1.6)^2`

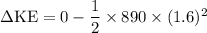
Step 2:

`\text{Work} = \Delta \text{KE} = - (1)/(2) * 890 * (1.6)^2`

Step 3:

`\text{Force} = \frac{\text{Work}}{d} = (- (1)/(2) * 890 * (1.6)^2)/(0.195)`

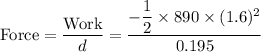
Now, let's calculate the magnitude of the average force:

`\text{Force} \approx (- 1427.2)/(0.195) \approx - 7319.59 \text{ N}`

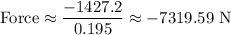
The magnitude of the average force on the bumper is approximately 7319.59 N. The negative sign indicates that the force is in the opposite direction to the initial motion of the car, which is necessary to bring the car to rest.