Final Answer:
Below.
In-depth explanation:
Hi! Let's solve this activity.
First of all, the 6 came from finding the least common denominator. I'm going to explain in detail what the process is.
The problem that we're asked to solve is:
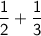
As you can see, we have two fractions with different denominators.
Since the fractions have different denominators, we can't just add the numerators, but we'll basically make the denominator the same.
Of course, in math, we can't just write any number we want. So to make the denominator the same, we'll perform some operation to it first.
We'll find the LCM (least common multiple) of 2 and 3. This process is called finding the least common denominator.
The LCM of 2 and 3 is 6 (this is where the 6 comes from!).
We multiplied 2 times 3 to reach 6. We do the same thing to the numerator:
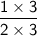

Next, we multiplied 3 by 2 to reach 6, so we do the same thing to the denominator:
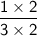

So, our addition problem is:
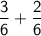

∴ the answer is 5/6.
