Question

Identify a counterexample to disprove 2n < n2 + 1, where n is a real number.

Answer 1

n = 1

Explanation:

To disprove the inequality 2n < n² + 1 (where n is a real number), we need to find a counterexample, which is a single value of "n" for which the inequality is not true.

Solve the inequality for n:

`\begin{aligned}2n & < n^2+1\\n^2+1& > 2n\\n^2-2n+1& > 0\\n^2-n-n+1& > 0\\n(n-1)-(n-1)& > 0\\(n-1)(n-1)& > 0\\(n-1)^2& > 0\end{aligned}`

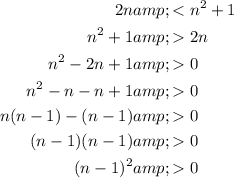
The inequality holds true for all real numbers n except when n = 1.

When n = 1, the expression (n - 1)² becomes (1 - 1)² which is equal to zero.

Therefore, the solution to the inequality is (-∞, 1) ∪ (1, ∞).

A counterexample is a one specific example that contradicts the proposed statement. Therefore, the counterexample to 2n < n² + 1 is n = 1, as when n = 1, the inequality does not hold true.

Answer 2

n = 1

Explanation:

A counter example to disprove
`\tt 2n < n^2 + 1` ,

where,

• n is a real number

We have

`\sf 2n < n^2 + 1`

subtracting both side by 2n

`\tt 0 < n^2 - 2n +1`

`\tt 0 < (n-1)^2`

`\textsf{Using formula: }\boxed{\sf a^2 - 2ab+ b^2 = (a-b)^2}`

`\tt 0 < (n-1)(n-1)`

when n =1,

(n-1)^2 =(1-1)^2 = 0

Which is not true.

2*1 < 1^2 +1

2 < 2

Since they are not true, which do not satisfy the inequality.

so, Counterexample to disprove is 1.

Therefore, The real number for a counterexample to disprove
`\tt 2n < n^2 + 1` is 1.