Answer:
Approximately
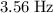 .
.
Step-by-step explanation:
Under the assumptions of this question, the object will be part of a spring-mass system and will be in a simple harmonic motion. To find the frequency of this motion, start by finding the effective spring constant. After that, derive the equation for the frequency of this spring-mass system. Substitute in the effective spring constant and the mass of the object to find the frequency of the motion.
Assume that two ideal springs of equal length are connected in parallel. The two springs would behave like one ideal spring with the spring constant equal to the sum of that of the two individual springs.
In this question, the spring constant of the two individual springs are
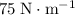 and
and
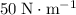 , respectively. When the two springs are connected as described, the effect of the two separate springs would be equivalent to that of one ideal spring with spring constant
, respectively. When the two springs are connected as described, the effect of the two separate springs would be equivalent to that of one ideal spring with spring constant
 .
.
Assume that the mass of the two springs are negligible. The expression for the frequency of this motion can be derived as follows:
In a frictionless horizontal spring-mass system, the net force on the moving object is equal to the restoring force from the spring. If the object is at a distance of
 from the equilibrium position, this restoring force would be
from the equilibrium position, this restoring force would be
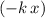 where
where
 is the spring constant. (Negative since this force is opposite in direction to displacement.)
is the spring constant. (Negative since this force is opposite in direction to displacement.)
Divide this net force by mass to obtain the acceleration
 of the moving object:
of the moving object:
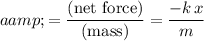 .
.
Assume that the moving object started at a distance of
 (amplitude) from the equilibrium position at time
(amplitude) from the equilibrium position at time
 .
.
Let
 denote the frequency of the motion. Since this object would be in a simple harmonic motion, position at time
denote the frequency of the motion. Since this object would be in a simple harmonic motion, position at time
 would be
would be
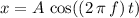 . The acceleration at time
. The acceleration at time
 would be
would be
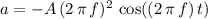 .
.
Substitute the expressions for
 and for
and for
 into the equation
into the equation
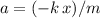 to obtain:
to obtain:
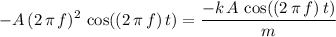 .
.
Simplify to obtain an expression for the frequency
 of the motion given the spring constant
of the motion given the spring constant
 and mass
and mass
 :
:
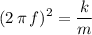 .
.
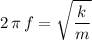 .
.
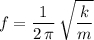 .
.
Ensure that mass is measured in the standard unit of kilograms:
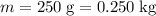 . Substitute the value of mass and the effective spring constant
. Substitute the value of mass and the effective spring constant
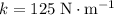 into the expression for frequency
into the expression for frequency
 and evaluate:
and evaluate:
 .
.
In other words, the frequency of this motion would be approximately
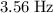 .
.