Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1.
`50\pi/3\approx157`

2.
`3\pi`

3.
`20\pi/3\approx 20.9`

Explanation:

1. A 60° arc is 1/6 of the circumference of a full circle. Because the diameter of the circle is 100 ft., the circumference is
`100\pi`. 1/6 of this value is
`50\pi/3`.

2. Since the diameter is 12, the radius is 6 and the area is
`36\pi`. Since the cake is cut in 12 pieces, the area of each is
`3\pi`.

3. 5 hours out of 12 is 5/12 of the circle's circumference. The circumference of the circle is
`16\pi`, so the watch's hand travels
`20\pi/3`.

Answer 2

1) 52 ft

2) d. 3π square inches

3) 20.9 inches

Explanation:

Question 1

Jim's pool is circular with a diameter of 100 ft.

The radius of a circle is half its diameter. Therefore, the radius of the pool is r = 50 ft.

To find the length of the arc Jim swims, we can use the arc length formula:

`\boxed{\begin{minipage}{6.4 cm}\underline{Arc length}\\\\Arc length $= \pi r\left((\theta)/(180^(\circ))\right)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

Given Jim travels an arc of 60°, substitute θ = 60° into the equation, along with r = 50 and π = 3.14:

`\begin{aligned}\textsf{Arc length}&= \pi r\left((\theta)/(180^(\circ))\right)\\\\&= 3.14 \cdot 50\left((60^(\circ))/(180^(\circ))\right)\\\\&=157\left((1)/(3)}\right)\\\\&=52.33333...\\\\&=52\sf \; ft\;(nearest\;foot)\end{aligned}`

Therefore, if Jim swims a 60 degree arc, he travels 52 ft (nearest foot).

`\hrulefill`

Question 2

To find the area of each slice of Rachel's cake, we need to calculate the total area of the cake and then divide it by the number of pieces she plans to cut it into.

The cake is circular, and its diameter is given as 12 inches. The radius of a circle is half its diameter. Therefore, the radius of the cake is r = 6 inches.

The formula to find the area of a circle is:

`\large\boxed{\textsf{Area} = \pi r^2}`

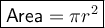
Substitute the radius r = 6 into the area formula to find the area of the cake:

`\begin{aligned}\textsf{Area of the cake}&=\pi \cdot 6^2\\&=36\pi \sf \; ft^2\end{aligned}`

To find the area of each slice given that Rachel plans to cut the cake into 12 pieces, divide the total area of the cake by 12:

`\begin{aligned}\textsf{Area of each slice}&=(\sf Total\;area)/(\sf Number\;of\;pieces)\\\\&=(36\pi)/(12)\\\\&=3\pi \; \sf ft^2\end{aligned}`

Therefore, each slice of Rachel's chocolate cake has an area of 3π square inches.

`\hrulefill`

Question 3

To calculate how far the hour hand of a clock travels during 5 hours, we need to calculate the arc length covered by the hour hand in that time.

The hour hand completes one full rotation in 12 hours, which is equivalent to 360°. Therefore, the angle covered by the hour hand in 5 hours is 5/12 of 360°:

`\theta=(5)/(12) \cdot 360^(\circ)=150^(\circ)`

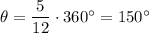
The given diameter of the clock is 16 inches. The radius of a circle is half its diameter. Therefore, the radius of the clock is r = 8 inches.

To calculate the arc length, substitute the found angle, θ = 150°, the radius, r = 8, and π = 3.14 into the arc length formula:

`\begin{aligned}\textsf{Arc length}&= \pi r\left((\theta)/(180^(\circ))\right)\\\\&= 3.14 \cdot 8\left((150^(\circ))/(180^(\circ))\right)\\\\&=25.12\left((5)/(6)\right)\\\\&=20.933333...\\\\&=20.9\sf \; in\;(nearest\;tenth)\end{aligned}`

Therefore, the hour hand of the clock travels approximately 20.9 inches during 5 hours.