Question

Which is equivalent to 4√9^(1/2)x

9^2x
9^(1/8)x
√9^x
6√9^x

Answer 1

`\sf \sqrt[4]{9}^{(1)/(2)x} \textsf{ is equivalent to: }\boxed{9^{(1)/(8)x}}`

Explanation:

To simplify the expression
`\sf \sqrt[4]{9}^{(1)/(2)x}`, we can use the properties of exponents and radicals.

let's rewrite
`\sf \sqrt[4]{9}` as a fractional exponent:
`\boxed{ \sf \sqrt[a]{b} = b^{(1)/(a)}}`

`\sf \sqrt[4]{9} = 9^{(1)/(4)}`

Now, we can apply the power of a power property, which states that
`\boxed{\sf (a^m)^n = a^(m \cdot n)}:`

`\sf (9^{(1)/(4)})^{(1)/(2)x}= 9^{(1)/(4) \cdot (1)/(2)x}`

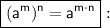
Simplifing the exponent:

`\sf (1)/(4) \cdot (1)/(2)x = (1)/(8)x`

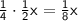
So, the expression becomes:

`\sf 9^{(1)/(4) \cdot (1)/(2)x} = 9^{(1)/(8)x}`

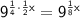
Now, we have the expression equivalent to
`\sf \sqrt[4]{9}^{(1)/(2)x} \textsf{ as } 9^{(1)/(8)x}`