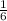Question

What is the solution to –2(8x – 4) < 2x + 5?

x > x is greater than StartFraction 1 Over 6 EndFraction.
x < x is less than StartFraction 1 Over 6 EndFraction.
x > 6
x < 6

Answer 1

Given to us:–

• an inequality
  `\mathsf{-2(8x - 4) < 2x + 5}`

To find:–

• x = ??

First , Use the distributive property :

`\bf{-2 (8x - 4) < 2x + 5}`

`\bf{-16x+8 < 2x+5}`

Subtract 2x from both sides :

`\bf{-16x - 2x + 8 < 5}`

`\bf{-18x + 8 < 5}`

Subtract 8 from both sides :

`\bf{-18x < 5-8}`

`\bf{-18x < -3}`

Divide each side by -18 :

`\bf{x > (3)/(18)}`

`\bf{x > (1)/(6)}`

Henceforth , x > 1/6 .

Answer 2

x >
`(1)/(6)`

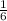
Explanation:

- 2(8x - 4) < 2x + 5 ← distribute parenthesis on left side

- 16x + 8 < 2x + 5 ( subtract 2x from both sides )

- 18x + 8 < 5 ( subtract 8 from both sides )

- 18x < - 3

divide both sides by - 18, reversing the symbol as a result of dividing by a negative quantity.

`(-18)/(-18)` x >
`(-3)/(-18)` , that is

x >
`(1)/(6)`