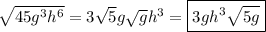Question

ASAP HELP PLEAAEE!!!!
ALGEBRA 1A

Answer 1

`3gh^3√(5g)`

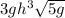
Explanation:

Given radical expression:

`√(45g^3h^6)`

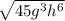
A perfect square is a number that can be expressed as the square of an integer. For example, 16 is a perfect square as it can be expressed as the square of 4: 16 = 4².

A factor pair of 45 is 9 and 5. Therefore, √(45) can be written as the product of two square root factors, √9 and √5.

As 9 is a perfect square (9 = 3²), and according to the radical rule, √(a²) = a, √9 can be simplified to √(3²) = 3:

`√(45)=\boxed{√(9)√(5)}=\boxed{3√(5)}`

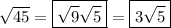
According to the exponent product rule, when you multiply two terms with the same base, you can combine their exponents by adding them together. Therefore, we can rewrite g³ as g²⁺¹ = g² × g.

Therefore, √(g³) can be rewritten as the product of two square root factors, √(g²) and √g. As g² is a perfect square, √(g²) can be simplified to g:

`√(g^3)=\boxed{√(g^2)√(g)}=\boxed{g√(g)}`

According to the exponent product rule, when you multiply two terms with the same base, you can combine their exponents by adding them together. Therefore, we can rewrite h⁶ as h²⁺²⁺² = h² × h² × h².

Therefore, √(h⁶) can be rewritten as the product of three square root factors, √(h²) and √(h²) and √(h²). As h² is a perfect square, √(h²) can be simplified to h:

`√(h^6)=\boxed{√(h^2)√(h^2)√(h^2)}=\boxed{h^3}`

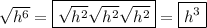
Combine the answers from the previous steps to write the simplified form of the given radical expression:

`√(45g^3h^6)=3√(5)g√(g)h^3=\boxed{3gh^3√(5g)}`