Question

Consider the line y = 3-9x. What is the slope of a line parallel to this line? What is the slope of a line perpendicular to this line? Slope of a parallel line: Slope of a perpendicular line: ​

Answer 1

Given to us:–

• a line y = 3 - 9x

To find:–

• Slope of the line perpendicular to y = 3 - 9x
• Slope of the line parallel to y = 3 - 9x

We will start by rewriting the equation :

➱
`\sf{y=-9x+3}`

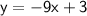
Now , The important thing to realise is that parallel lines have the same slope . Therefore , The line parallel to y = -9x + 3 will have the same slope as y = -9x + 3 . That slope is -9 .

With perpendicular lines , slopes are negative reciprocals of one another . Therefore , The slope of the line perpendicular to y = -9x + 3 will be the negative inverse of the slope of the above line .

➱ The negative inverse of -9 is 1/9 .

Henceforth , The slope of a parallel line is -9 , and the slope of a perpendicular line is 1/9 .

Answer 2

- 9 and
`(1)/(9)`

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

given

y = 3 - 9x = - 9x + 3 ← in slope- intercept form

with slope m = - 9

• Parallel lines have equal slopes

• slope of a parallel line is then m = - 9

given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(-9)` =
`(1)/(9)`

• slope of a perpendicular line is then m =
`(1)/(9)`