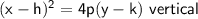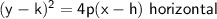Answer:
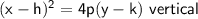
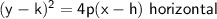
Explanation:
The orientation of the axis of symmetry of a parabola in standard form can be determined by the form of the equation.
If the equation is in the form of
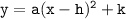 , then the axis of symmetry is vertical, and the equation of the axis is x=h.
, then the axis of symmetry is vertical, and the equation of the axis is x=h.
If the equation is in the form of
 then the axis of symmetry is horizontal, and the equation of the axis is y=k.
then the axis of symmetry is horizontal, and the equation of the axis is y=k.
The equations you provided are:
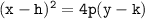
(y-k)^2 = 4p(x − h)
In the first equation, the x term is squared, so the axis of symmetry is Vertical.
In the second equation, the y term is squared, so the axis of symmetry is Horizontal.
Therefore, the answers are: