Answer:
-2
Explanation:
The vertex of the quadratic function is (6, 2), so h = 6 and k = 2.
The y-intercept of the function is (0, -70),
so we can substitute these values into the equation
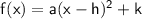 to get:
to get:
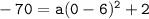
Solving bracket 1st.
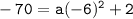
subtracting both side by 2
-70-2 = 36a
-72 = 36a
dividing both side by 36.
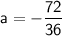
a = -2
Therefore, the value of a is -2.