Question

Write the slope-intercept equation of the function f whose graph satisfies the given conditions.

The graph of f passes through (-5,-4) and is perpendicular to the line whose equation is x= 1.
The equation of the function is

Answer 1

f(x) = -4

Explanation:

Pre-Solving

We are given that function f passes through (-5,-4) and is perpendicular to the line x = 1.

We want to write the equation of this function in slope-intercept form.

Slope-intercept form is given as f(x) = mx + b, where m is the slope and b is the y-intercept.

Recall that perpendicular lines have slopes that are negative and reciprocal.

Solving

Slope

So, we need to find the slope of x = 1. It is a vertical line, which means that the line is undefined.

We can write this undefined slope as
`(1)/(0)`.

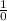So, the negative and reciprocal slope of
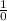`(1)/(0)` would be
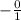`-(0)/(1)`, which is just 0.

Equation

So, we can plug 0 as m in f(x) = mx + b.

We get:

f(x) = 0x + b

Now, we need to find b.

As the line passes through (-5, -4), we can plug the values into the equation.

Substitute -5 as x and -4 as f(x).

-4 = 0(-5) + b

Multiply.

-4 = b

Substitute -4 as b.

f(x) = 0x -4

We can rewrite this as:

f(x) = -4