Question

​A bacteria culture containing 370​ bacteria is started in a petri dish. After 3​ hours, the bacteria population has grown to 555​. Assume the bacteria growth is exponential.

Answer 1

Explanation:

Not sure what you are looking for....there is no question in your post

370 e^kt = 555

370 e^k(3) = 555

k=.135155

# of bacteria after 't' hours = 370 e^(.135155 * t)

Answer 2

`r = 0.14\;\sf(2\;d.p.)`

`P(t) = 370 e^(0.14t)`

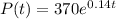
Explanation:

To find the growth rate of the bacteria, we can use the exponential growth formula, which is given by:

`\large\boxed{P(t)=P_0e^(rt)}`

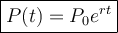
where:

• P(t) is the population of bacteria at time t.
• P₀ is the initial population of bacteria (at t = 0).
• e is the base of the natural logarithm (Euler's number).
• r is the growth rate (per unit time).
• t is the time in hours.

Given that the initial population is 370 bacteria, then P₀ = 370.

If the population after 3 hours is 555 bacteria, then P(3) = 555.

Substituting these values into the formula, we get:

`555 = 370 e^(3r)`

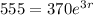
Solve for r:

`\begin{aligned}555 &= 370 e^(3r)\\\\(555)/(370) &= e^(3r)\\\\\ln \left((555)/(370)\right) &= \ln \left(e^(3r)\right)\\\\\ln \left((555)/(370)\right) &= 3r \ln \left(e\right)\\\\\ln \left((555)/(370)\right) &= 3r \\\\r&=(1)/(3)\ln \left((555)/(370)\right)\\\\r&=0.135155036...\\\\r&=0.14\; \sf (2\;d.p.)\end{aligned}`

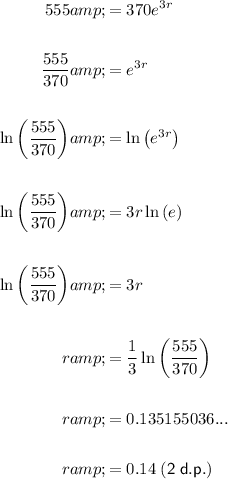
So, the growth rate of the bacteria is approximately 0.14 (rounded to 2 decimal places).

Now that we know the growth rate (r), we can create a model for the population of bacteria at any time t by substituting the given initial population, P₀ = 370, and the found growth rate, r = 0.14:

`\large\boxed{P(t) = 370 e^(0.14t)}`

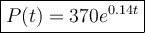
This model gives the population of bacteria (P) at any time t (in hours) after starting with an initial population of 370 bacteria.