Answer:
226°
Explanation:
According to the Tangent and Intersected Chord Theorem, if a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one-half the measure of its intercepted arc.
Therefore, if y = 113°, then y is one-half of the intercepted arc x.:
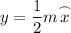
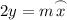
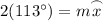
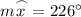
Therefore, the measure of arc x is 226°.