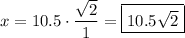Question

Special right triangles

Please help I don’t understand this at all step by step would be super appreciated

Answer 1

`x = 10.5\sqrt2`

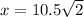
Explanation:

We can solve for side length x in this compound triangle by using the ratios of the side lengths of 30-60-90 and 45-45-90 right triangles:

• 30-60-90: 1 - √3 - 2
• 45-45-90: 1 - 1 - √2

We are given that the length of the hypotenuse (the longest side) of the 30-60-90 triangle is 7√3. This corresponds to 2 in the side lengths ratio.

To solve for the altitude of the compound triangle (the side shared by the two smaller triangles), we can multiply this hypotenuse length by the ratio of the longer leg (the second longest side) to the hypotenuse. Here is that logic in equation form:

`\text{hyp} * \frac{\text{long leg}}{\text{hyp}} = \text{long leg}`

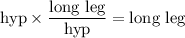
↓ plugging in the hypotenuse length and side lengths ratio

`7\sqrt3 * (\sqrt3)/(2)`

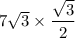
↓ grouping like factors

`(7)/(2) * \sqrt3\sqrt3`

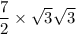
↓ simplifying

`3.5 * 3`

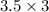
↓ executing the multiplication

`10.5`

So, the length of the altitude is 10.5.

Finally, we can multiply this length by the side lengths ratio for the 45-45-90 triangle to solve for side length x.

`x = 10.5 \cdot (\sqrt2)/(1) = \boxed{10.5\sqrt2}`