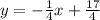Answer:
Point-slope form:
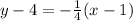
Slope-intercept form:
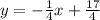
Explanation:
Pre-Solving
We are given that one line has the equation y = 4x.
We also know that line L is perpendicular to y = 4x, and that both lines passes through (1,4).
We want to write the equation of line L in point-slope form and slope-intercept form.
Point-slope form is
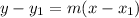 where m is the slope and
where m is the slope and
 is a point.
is a point.
Slope-intercept form is y=mx+b, where m is the slope and b is the value of y at the y-intercept.
Also recall that perpendicular lines have slopes that multiply to equal -1.
Solving
Slope
First, we need to get the slope of y=4x.
Notice how the line is in slope-intercept form, and that 4 is in the place of where m is in mx.
This means that the slope of this line is 4.
Now, we need to find the slope of the perpendicular line.
As already stated, perpendicular lines multiply to equal -1.
So, we can say:
4m = -1
Divide both sides by 4.
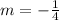
This is the slope of line L.
Point-Slope Form
Let's find the equation of line L in point-slope form.
As we now found the slope of this line, we can substitute that value of that line into the formula.
We get:
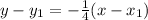
Now, substitute 1 as
 and 4 as
and 4 as
 .
.
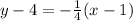
Slope-Intercept Form
Now, let's find the equation of line L in slope-intercept form.
We can take take the point-slope form that we found earlier to get into slope-intercept form. We can notice that in slope-intercept form, we have only y on one side.
We can start by distributing -1/4 to both x and -1 on the right side.
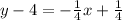
Now, add 4 to both sides.