Question

Solve and explain question

Answer 1

(a) 14 m

(b) 5.39 m

Explanation:

Part (a): To find the horizontal distance that the balloon traveled, we need to determine the value of "x" when the height "h" is zero. This is because at the maximum height point, the water balloon will eventually fall back to the ground, where its height is zero.

Given the equation: h = -0.11x² + 1.54x

When the water balloon reaches its maximum height, h = 0, so we can set the equation to zero:

⇒ 0 = -0.11x² + 1.54x

Now, we need to solve this quadratic equation for "x." There are several methods to do this, such as factoring, completing the square, or using the quadratic formula. Let's use the quadratic formula:

The quadratic formula states that for an equation of the form ax² + bx + c = 0, the solutions for "x" are given by:

`\boxed{\left\begin{array}{ccc}\text{\underline{Quadratic Formula:}}\\\\x=(-b \pm √(b^2-4ac))/(2a) \end{array}\right}`

In our case, a = -0.11, b = 1.54, and c = 0.

`\Longrightarrow x=(-1.54 \pm √((1.54)^2-4(-0.11)(0)))/(2(-0.11))`

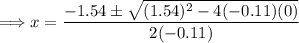
Now, let's calculate the values:

`\Longrightarrow x_1=(-1.54 + √((1.54)^2-4(-0.11)(0)))/(2(-0.11))\\\\\\\\\Longrightarrow x_1=(-1.54 + √(2.3716-0))/(-0.22)\\\\\\\\\Longrightarrow x_1=(-1.54 + 1.54)/(-0.22)\\\\\\\\\Longrightarrow x_1=(0)/(-0.22)\\\\\\\\\therefore x_1=0`

____

`\Longrightarrow x_2=(-1.54 - √((1.54)^2-4(-0.11)(0)))/(2(-0.11))\\\\\\\\\Longrightarrow x_2=(-1.54 - √(2.3716-0))/(-0.22)\\\\\\\\\Longrightarrow x_2=(-1.54 - 1.54)/(-0.22)\\\\\\\\\Longrightarrow x_2=(-3.08)/(-0.22)\\\\\\\\\therefore x_2=14`

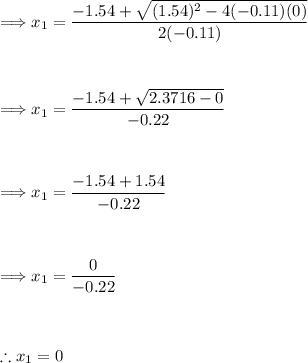
Now, we have two possible values for "x": x = 0 and x = 14. The value x = 0 indicates the initial position of the water balloon when the height is also zero. Logically, this makes sense. The water balloon will start at h = 0, x = 0 and end at h = 0, x = '??'.

The value x = 14 indicates the final position of the water balloon. Thus, the water balloon traveled a horizontal distance of 14 meters.

Part (b): To find the maximum height reached by the water balloon, we substitute the value of "(1/2)x" corresponding to the maximum height into the equation for "h":

⇒ h = -0.11x² + 1.54x

The path of travel the water balloon takes will represent a parabola. Thus, when the balloon has traveled 7 meters its height will be the greatest.

Now we can calculate the height "h":

⇒ h = -0.11(7)² + 1.54(7)

⇒ h = -0.11(49) + 10.78

⇒ h = -5.39 + 10.78

∴ h = 5.39 m

So, the maximum height reached by the water balloon is 5.39 meters.

`\hrulefill`

Additional Information:

We can check if our answers are correct by typing the function "h" into a graphing calculator. Refer to the attached image.