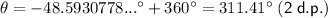Question

Solve the following for
0 < Theta < 360


sin theta + 3/4 = 0

Answer 1

θ = 311.41°

θ = 228.59°

Explanation:

To solve the trigonometric equation sin(θ) + 3/4 = 0 for the given interval 0° < θ < 360°, we can use algebraic manipulation and inverse trigonometric functions.

Isolate sin(θ) by subtracting 3/4 from both sides of the equation:

`\begin{aligned}\sin \theta+(3)/(4)&=0\\\\\sin \theta+(3)/(4)-(3)/(4)&=0-(3)/(4)\\\\\sin \theta &= -(3)/(4)\end{aligned}`

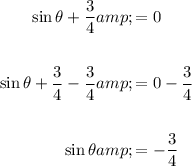
Take the inverse sine (arcsin) of both sides to solve for θ:

`\begin{aligned}\arcsin \left(\sin \theta\right) &=\arcsin \left( -(3)/(4)\right)\\\\\theta&=-48.5903778...^(\circ)\end{aligned}`

A positive angle is measured counterclockwise from the positive x-axis, whereas a negative angle is measured clockwise from the positive x-axis. Therefore, θ is in quadrant IV.

As sine is negative in quadrants III and IV, the other value of θ when sinθ = -3/4 is in quadrant III. Therefore, to find the other solution, add 180° to the initial solution:

`\theta=-48.5930778...^(\circ) + 180^(\circ) = 228.5903778...^(\circ)`

The sine function is periodic with a period of 360°. Therefore, the solutions are:

`\theta = -48.5930778...^(\circ) + 360^(\circ)n`

`\theta = 228.5903778...^(\circ) + 360^(\circ)n`

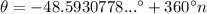
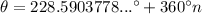
Therefore, the solutions for the given equation in the interval 0° < θ < 360° are:

`\theta = -48.5930778...^(\circ) + 360^(\circ) = 311.41^(\circ) \; \sf(2\;d.p.)`

`\theta = 228.5903778...^(\circ) = 228.59^(\circ) \; \sf(2\;d.p.)`

Answer 2

`\tt \Theta \approx 228.59^\circ \quad \text{and} \quad \Theta \approx 311.41^\circ`

Explanation:

Let's solve the trigonometric equation for
`\tt 0 < \theta < 360^\circ`

`\tt \sin(\Theta) + (3)/(4) = 0`

We can follow these steps:

Subtract
`(3)/(4)` from both sides to isolate sin θ.

`\tt \sin(\Theta) = -(3)/(4)`

Find the inverse sine (or arcsin) of both sides to find the possible values of θ.

`\tt \Theta = \arcsin\left(-(3)/(4)\right)`

Using a calculator to compute the arcsin and find the principal value of θ.

(since we're looking for values in the range
`\tt 0 < \Theta < 360^\circ`)

`\tt \Theta \approx -48.59^\circ \quad`

Since
`\tt \sin(\Theta)` is negative in both the third and forth quadrants, we can find the other solutions by adding 180° to the principal value:

`\tt \Theta = 180^\circ + 48.59^\circ \approx 228.59^\circ`

`\tt \Theta = 360^\circ - 48.59 ^\circ \approx 311.41^\circ`

Therefore,

The solutions for
`0 < \Theta < 360^\circ` are approximately:

`\tt \Theta \approx 228.59^\circ \quad \text{and} \quad \Theta \approx 311.41^\circ`