Question

Can someone please do the whole page ?? please !


(show work)

Answer 1

Graph is a parabola which opens upwards.

Explanation:

The graph of the quadratic function
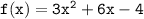`\tt f(x) = 3x^2 + 6x - 4` can be graphed by plotting points and connecting them with a smooth curve.

To start, we can create a table of values to plot points on the coordinate plane.

Let's calculate some values of f(x) for different x values:

`\boxed{\begin{array}c x& f(x) = 3x^2 + 6x - 4\h \\-3 & 5 \\-2 & -4 \\-1 & -7 \\0 & -4 \\1 & 5 \\\end{array}}`

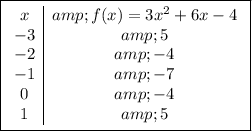
Now, let's plot these points on the coordinate plane:

when we keep the value of x, we get y and these points are:

• Point A: (-3, 5)
• Point B: (-2, -4)
• Point C: (-1, -7)
• Point D: (0, -4)
• Point E: (1, 5)

Now, Plot it in graph.

The graph of the quadratic function f(x) = 3x^2 + 6x - 4 has the following features:

• The vertex of the parabola is at (-1, -7)
• The parabola opens upwards.
• The axis of symmetry is the line x = -1
• The minimum value of the function is f(-1) = -7.