Question

Can someone please do the whole page ?? please !
(show work)

Answer 1

14.

`\boxed{\begin{aligned}&\textsf{A. Discriminant} = 64 \\&\textsf{B. 2 Real solutions} \\&\textsf{C. If solutions exist:}\\&x = 5 \\ &x = -3\end{aligned}}`

15.

`\boxed{\begin{aligned}&\textsf{A. Discriminant} = -131 \\&\textsf{B. No Real solutions} \end{aligned}}`

Explanation:

Solution for question no. 14

`\tt 14. \:x^2-2x -15 =0`

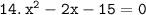
Comparing above equation with
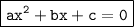`\boxed{\tt ax^2+bx +c =0}`,we get

• a = 1
• b = -2
• c = -15

a) Finding the discriminant

The discriminant of a quadratic equation is
`\boxed{\tt b^2 - 4ac}`, where a, b, and c are the coefficients of the equation.

Substituting value of a, b and c, we get

`\textsf{Discriminant }\tt =(-2)^2 - 4(1)(-15) = 4 + 60 = 64`

Therefore, Discriminants is 64.

b) State it's solutions:

The number of real solutions of a quadratic equation depends on the value of the discriminant.

• If the discriminant is positive, then there are two real solutions.
• If the discriminant is 0, then there is one repeated real solution.
• If the discriminant is negative, then there are no real solutions.

In this case, the discriminant is positive, so there are two real solutions.

c) If solutions exist, use the quadratic formula to solve for all solutions of x.

The quadratic formula is a formula that can be used to solve any quadratic equation.

The formula is:

`\tt x = (-b \pm √(b^2 - 4ac))/(2a)`

In this case, the coefficients are a=1, b=-2, and c=-15.

So, the quadratic formula gives us the following solutions:

`\tt x = (-(-2) \pm √((-2)^2 - 4(1)(-15)))/( 2(1))`

`\tt x = (2 \pm √(4 + 60))/(2)`

`\tt x = (2 \pm √(64))/(2)`

`\tt x = (2 \pm 8)/(2)`

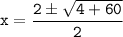
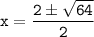
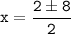
Either

`\tt x = (2 + 8)/(2) =5`

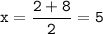
or

`\tt x = (2 - 8)/(2) =-3`

Therefore, x = 5 or -3

In summary:

A. Discriminant = 64

B. 2 Real solutions

C. If solution exist:

x = 5

x = -3

`\hrulefill`

Similarly, Let's do another.

`\tt 15. \:\:3x^2+x+11 =0`

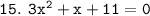
Comparing above equation with
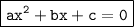`\boxed{\tt ax^2+bx +c =0}`,we get

• a = 3
• b = 1
• c = 11

a) Finding the discriminant

The discriminant of a quadratic equation is
`\boxed{\tt b^2 - 4ac}`, where a, b, and c are the coefficients of the equation.

Substituting value of a, b and c, we get

`\textsf{Discriminant }\tt =(1)^2 - 4(3)(11) = 1-132=-131`

Therefore, Discriminants is -131.

b) State it's solutions:

The number of real solutions of a quadratic equation depends on the value of the discriminant.

• If the discriminant is positive, then there are two real solutions.
• If the discriminant is 0, then there is one repeated real solution.
• If the discriminant is negative, then there are no real solutions.

In this case, the discriminant is positive, so there are no real solutions.

c)Although, No solutions exist, let's use the quadratic formula to solve for all solutions of x.

The quadratic formula is a formula that can be used to solve any quadratic equation.

The formula is:

`\tt x = (-b \pm √(b^2 - 4ac))/(2a)`

In this case, the coefficients are a=3, b=1, and c=11.

So, the quadratic formula gives us the following solutions:

`\tt x = (-1\pm √((1)^2 - 4(3)(11)))/( 2(3))`

`\tt x = (2 \pm √(-131))/(2)`

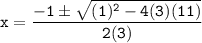
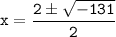
either

`\tt x = (2 + √(-131))/(2)`

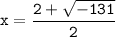
or
`\tt x = (2 - √(-131))/(2)`

In summary:

A. Discriminant = -131

B. No Real solutions