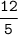Question

Express tan O as a fraction in simplest terms.
M
12
13
N
O

Answer 1

`\tt \textsf{Tan O }=(12)/(5)`

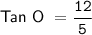
Explanation:

Given:

In right angled triangle MNO with respect to ∡O

Perpendicular [p] = MN = 12

Base [b} = ON

Hypotenuse [h] = OM = 13

Tan O = ?

Solution:

The tangent of an angle in a right triangle is the ratio of the perpendicular to the base. The perpendicular is the side that is opposite the angle, and the base is the side that is adjacent to the angle.

Here,

`\tt Tan O = (Perpendicular)/(Base)`

`\tt Tan O = (MN)/(ON)`

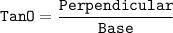
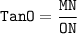
Since, we do not have value of ON,

We can find it by using Pythagoras rule:

The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

`\boxed{\tt h^2 = p^2+b^2}`

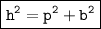
Substituting value,

`\tt 13^2 = 12^2 + b^2`

`\tt 169 = 144 + b^2`

`\tt b^2 = 169 - 144`

`\tt b^2 = 25`

`\tt b=√(25)`

`\tt b= 5`

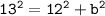
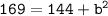
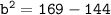
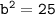
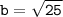
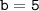
Therefore, value of ON is 5.

Now,

Substituting value of MN and ON is Tangent rule,

we get

`\tt Tan O = (12)/(5)`

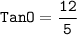
Therefore, Tan O as a simplest terms =
`\tt (12)/(5)`