Question

The hypotenuse of a right triangle is twice the length of one of its legs. Th length of the other leg is 12 feet. Find the lengths of three sides (in feet).

Answer 1

Given to us that:–

• The hypotenuse of a triangle is twice the length of one of its legs
• The length of the other leg is 12 ft

Step by step:–

The three sides are :

• 12 ft
• unknown
• twice the length of the unknown

Let x represent the unknown angle. Then the hypotenuse is 2x .

By using Pythagoras' identity,

`\bf{a^2+b^2=c^2}`

Substituting the known values ,

`\bf{12^2+x^2=(2x)^2}`

Simplifying,

`\bf{144+x^2=4x^2}`

Collect like terms,

`\bf{4x^2=x^2+144}`

`\bf{4x^2-x^2=144}`

`\bf{3x^2=144}`

Divide each side by 3 :

`\bf{x^2=144/3}`

`\bf{x^2=48}`

Square-root both sides :

`\bf{x\approx6.9\:ft}`

Then, the hypotenuse = 2 × 6.9 = 13.8 ft .

Henceforth, The sides are 6.9, 12, and 13.8 ft .

Answer 2

lengths of the three sides of the triangle are 7 feet, 12 feet, and 14 feet.

Explanation:

Let x be the length of the leg.

The hypotenuse is twice the length of this leg, so the hypotenuse has length 2x.

The other leg is 12 feet.

We can use the Pythagorean theorem to find the lengths of the three sides of the triangle.

The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

`\boxed{ \tt c^2 = a^2+b^2}`

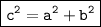
In this case, we have

• Hypotenuse(c)= 2x
• Leg(a) = x
• other leg(b) = 12 feet

Substituting value

`\tt \tt (2x)^2 = x^2 + 12^2`

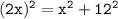
Simplifying the equation, we get:

`\tt 4x^2 = x^2 + 144`

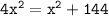
Subtracting x^2 from both sides, we get:

`\tt 4x^2 -x^2 = 144`

`\tt 3x^2 = 144`

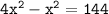
Dividing both sides by 3, we get:

`\tt x^2 =(144)/(3)`

`\tt x^2 = 48`

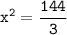
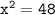
Taking the square root of both sides, we get:

`\tt x = √(48)`

`\tt x =7\textsf{ in 0 d.p}`

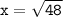
Therefore, length of leg is 7 feet.

The length of the hypotenuse is twice the length of this leg, so the hypotenuse has length 2 * 7=14 feet

Therefore, the lengths of the three sides of the triangle are 7 feet, 12 feet, and 14 feet.