Answer:

Explanation:
The general form of an exponential function is:
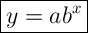
where:
- a is the initial value (y-intercept).
- b is the base (growth/decay factor) in decimal form.
To find the formula for an exponential function that passes through points (-1, 9/2) and (3, 72), substitute both points into the formula to create two equations in terms of a and b:


Divide equation 2 by equation 1 to eliminate a, then solve for b:
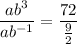
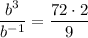
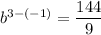
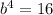
![b=\sqrt[4]{16}](https://img.qammunity.org/2024/formulas/mathematics/high-school/u2z6baxi0toyukwlvh42e6gac98junlcsk.png)

Therefore, the value of b is 2.
Substitute the found value of b into the second equation, and solve for a:
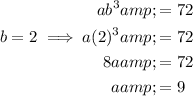
Therefore, the value of a is 9.
Therefore, the formula for an exponential function that passes through points (-1, 9/2) and (3, 72) is:
