Question

Find the sum of the first 45 terms of the following series, to the nearest integer. 2 , 11 , 20 , . .

Answer 1

Sum of the first 45 terms is 9000.

Explanation:

The given series is an arithmetic series, which means that the difference between any two consecutive terms is constant.

Solution:

The sum of an arithmetic series can be calculated using the following formula:

`\boxed{\tt S_n = (n)/(2)(2a+(n-1)d)}`

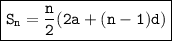
where:

• Sn is the sum of the arithmetic series.
• n is the number of terms
• a is the first term.
• d is the common difference

In this case,

• 1st term(a) = 2
• difference(d) = 11-2 =9

To find:

• Sum of 45 terms
• n =45

Plugging these values into the formula, we get the following:

`\tt S_(45) = (45)/(2)(2*2+(45-1)9)`

`\tt S_(45) = (45)/(2)(4+44*9)`

`\tt S_(45)= (45)/(2)(400)`

`\tt S_(45) = 45*200`

`\tt S_(45) = 9000`

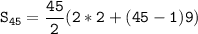
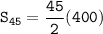
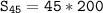
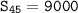
Therefore, The sum of the first 45 terms is 9000.