Question

A 3.00 kg block moving 2.09 m/s

right hits a 2.22 kg block moving
3.92 m/s left. Afterward, the
3.00 kg block moves 1.71 m/s left.
Find the velocity of the 2.22 kg
block afterwards.
(Unit = m/s)
Remember: right is +, left is -

Answer 1

Approximately
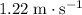`1.22\; {\rm m\cdot s^(-1)}` to the right.

Step-by-step explanation:

The velocity of the
`2.22\; {\rm kg}` block after the collision can be found using the conservation of momentum.

Before the collision:

• Velocity of the
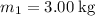  `m_(1) = 3.00\; {\rm kg}` block is
  `u_(1) = 2.09\; {\rm m\cdot s^(-1)}`.
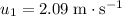• Velocity of the
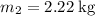  `m_(2) = 2.22\; {\rm kg}` block is
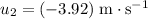  `u_(2) = (-3.92)\; {\rm m\cdot s^(-1)}` (negative since this block is moving to the left.)

After the collision:

• Velocity of the
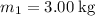  `m_(1) = 3.00\; {\rm kg}` block becomes
  `v_(1) = (-1.71)\; {\rm m\cdot s^(-1)}`.
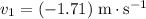• Velocity of the
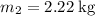  `m_(2) = 2.22\; {\rm kg}` block,
  `v_(2)`, needs to be found.

The momentum of an object is the product of its mass and velocity.

By the conservation of momentum:

`m_(1)\, u_(1) + m_(2)\, u_(2) = m_(1)\, v_(1) + m_(2)\, v_(2)`.

Rearrange and solve for
`v_(2)`:

`\begin{aligned} v_(2) &= (m_(1)\, u_(1) + m_(2)\, u_(2) - m_(1)\, v_(1))/(m_(2)) \\ &= ((3.00)\, (2.09) + (2.22)\, (-3.92) - (3.00)\, (-1.71))/(2.22)\; {\rm m\cdot s^(-1)} \\ &\approx 1.22\; {\rm m\cdot s^(-1)}\end{aligned}`.

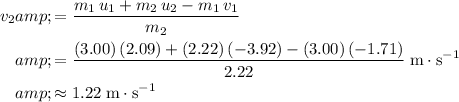In other words, the
`2.22\; {\rm kg}` block would be moving to the right (since
`v_(2)` is positive) at approximately
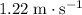`1.22\; {\rm m\cdot s^(-1)}` after the collision.