Question

To find the distance AB across a river, a distance BC=230 is laid off on one side of the river. It is found that B=109° and C=21°. Find AB using the law of sines.

Answer 1

AB ≈ 107.6

Explanation:

using the law of sines in Δ ABC

`(a)/(sinA)` =
`(b)/(sinB)` =
`(c)/(sinC)`

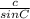
where a, b, c are sides opposite ∠ A, ∠ B, ∠ C

here a = BC = 230 and c = AB ( to be found )

we require to find ∠ A

the sum of the 3 angles in Δ ABC = 180°

∠ A + ∠ B + ∠ C = 180° , that is

∠ A + 109° + 21° = 180°

∠ A + 130° = 180° ( subtract 130° from both sides )

∠ A = 50°

using the following ratios to find AB

`(a)/(sinA)` =
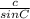`(c)/(sinC)` ( substitute values )

`(230)/(sin50)` =
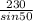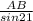`(AB)/(sin21)` ( cross- multiplying )

AB × sin50° = 230 × sin21° ( divide both sides by sin50° )

AB =
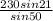`(230sin21)/(sin50)` ≈ 107.6 ( to 1 decimal place )