Question

Write the graphing form equation of a parabola with focus (3, -1) and directrix x = 5. Also include a sketch of the parabola. Show all your work.

Thank you!!

Answer 1

Hi,

Explanation:

equation parabola : (y-k)²=4p(x-h)

Focus=(3,-1)=(h+p,k)

directrix : x=h-p=5

h+p=3

h-p=5

=> h=4

p=-1

Equation is: (y+1)²=-4(x-4)

Answer 2

`(y + 1)^2 = -4(x - 4)`

Explanation:

To write the graphing form equation of a parabola with the given focus and directrix, we first need to determine whether the parabola opens horizontally or vertically.

The directrix of a parabola is a fixed line outside of the parabola that is perpendicular to the axis of symmetry.

Given that the directrix is a vertical line (x = 5), the parabola opens horizontally.

The standard equation of a parabola that opens horizontally is:

`\large\boxed{(y - k)^2 = 4p(x - h)}`

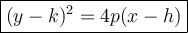
where

• p ≠ 0
• Vertex = (h, k)
• Focus = (h+p, k)
• Directrix: x = (h - p)
• Axis of symmetry: y = k

In this case, the focus is (3, -1). Therefore, k = -1.

The x-value of the vertex (h) is the midpoint between the x-values of the focus and the directrix. The x-value of the focus is 3 and the x-value of the directrix is 5. Therefore:

`h=(3+5)/(2)=4`

Therefore, the vertex is (4, -1).

To find the value of p, substitute the found value of h into the formula for the directrix:

`\begin{aligned}\textsf{Directrix:} \quad x&=h-p\\5&=4-p\\p&=4-5\\p&=-1\end{aligned}`

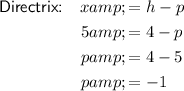
Substitute the values of h, k and p into the standard equation:

`\begin{aligned}{(y - k)^2 &= 4p(x - h)}\\\\\implies (y - (-1))^2 &= 4(-1)(x - 4)\\(y + 1)^2 &= -4(x - 4)\end{aligned}`

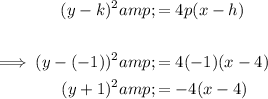
Therefore, the equation of the parabola in graphing form is:

`\large\boxed{\boxed{(y + 1)^2 = -4(x - 4)}}`

Find the y-intercepts of the parabola by substituting x = 0 into the equation:

`\begin{aligned}x=0 \implies (y + 1)^2 &= -4(0 - 4)\\(y + 1)^2& = -4(-4)\\(y + 1)^2 &= 16\\y+1 &= \pm 4\\y&=-1 \pm 4\\\\\implies y&=-5\\\implies y&=3\end{aligned}`

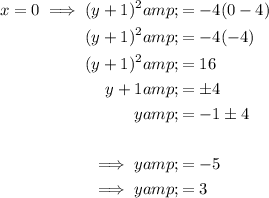
Therefore, the parabola crosses the y-axis at (0, -5) and (0, 3).

To sketch the graph of the parabola:

• Draw the directrix as a vertical line at x = 5.
• Plot the vertex at (4, -1).
• Plot the focus at (3, -1).
• Draw the axis of symmetry at y = -1.
• Plot the y-intercepts at (0, -5) and (0, 3).
• Draw a ⊃-shaped curve opening to the left passing through the y-intercepts and the vertex, symmetric about the axis of symmetry.