Question

3. Find the measure of side BC.

Answer 1

BC = 19.73

Explanation:

Given:

ABC is triangle.

AB = c = 23

AC = b = 26

∡A = 47°

To find:

BC = a =?

Solution:

We can use the Law of Cosines to solve for a.

The Law of Cosines states that for a triangle with side lengths a, b and c and angle measure A opposite side a, the following equation holds:

`\boxed{\tt a^2 = b^2 + c^2 - 2bc cos A}`

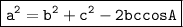
we can plug these values into the Law of Cosines to get the following equation:

`\tt a^2 = 26^2 + 23^2 - 2 \cdot 26 \cdot 23 \cos 47^\circ`

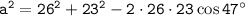
Evaluating the right side of the equation, we get:

`\tt a^2 = 1205 - 1196 \cos 47^\circ`

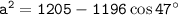
We can use the calculator to evaluate cos 47°.

The cosine of 47 degrees is approximately 0.682.

So we can approximate the right side of the equation as follows:

`\tt a^2 \approx 1205 - 1196\cdot 0.682 \approx 389.33`

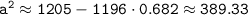
Taking the square root of both sides of the equation, we get:

`\tt a \approx √(389.33) \approx 19.73`

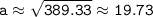
Therefore, the length of side BC is approximately 19.73 units